K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

MH
4 tháng 4 2017
Ý kiến đúng
Giả sử ngược lại y = f(x) + g(x) liên tục tại x0. Đặt h(x) = f(x) + g(x). Ta có g(x) = h(x) – f(x).
Vì y = h(x) và y = f(x) liên tục tại x0 nên hiệu của chúng là hàm số y = g(x) phải liên tục tại x0. Điều này trái với giả thiết là y = g(x) không liên tục tại x0.

NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 4 2020
a/ \(y=3x+2\)
b/ \(y=-\frac{1}{4}x+1\)
c/ \(y=\frac{1}{6}x+\frac{3}{2}\)
d/ \(y=-32x-48\)

4 tháng 4 2017
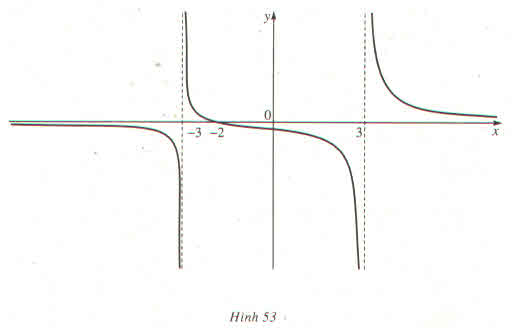
Quan sát đồ thị ta thấy x → -∞ thì f(x) → 0; khi x → 3- thì f(x) → -∞;
khi x → -3+ thì f(x) x → +∞.
b) f(x) =
=
= 0.
f(x) =
=
= -∞ vì
=
> 0 và
= -∞.
f(x) =
=
.
= +∞
vì
=
=
> 0 và
= +∞.

Đáp án đúng : B