Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Phương pháp: Dựa vào bảng biến thiên để xác định tiệm cận, cực trị, giá trị lớn nhất, giá trị nhỏ nhất.
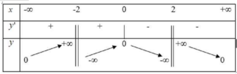
Cách giải: Dựa vào bảng biến thiên dễ thấy đồ thị hàm số có tiệm cận ngang y = 0 và hai tiệm cận đứng x = 2, x = -2. Vậy (I) sai và (IV) đúng.
Chọn C
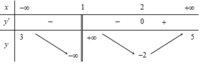
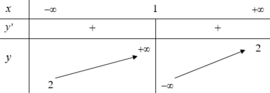
Từ bảng biến thiên ta thấy l i m x → + ∞ y = 5 ; l i m x → ∞ y = 3 đồ thị hàm số có hai đường tiệm cận ngang là y=5 và y=3. Và l i m x → 1 - y = - ∞ ⇒ x = 1 là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả là ba đường tiệm cận
Đáp án A
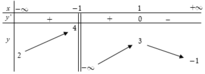
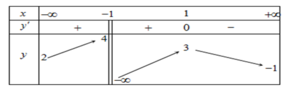
Vì hàm số không xác định tại x=-1 nên hàm số đồng biến trên ( - ∞ ; - 1 ) ; ( - 1 ; 1 ) .
Xét các khẳng định sau:
Đáp án C
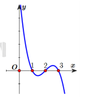
Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒ hàm số có 3 điểm cực trị
Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒ có 3 nghiệm phân biệt
Suy ra phương trình f x = m + 2018 có nhiều nhất 4 nghiệm
Xét y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2
Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).
Đáp án C
Các đường tiệm cận đứng là x = 1 ; x = − 1.
Tiệm cận ngang là
y
=
−
2
Vậy có tất cả 3 đường tiệm cận
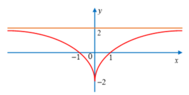
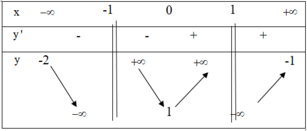
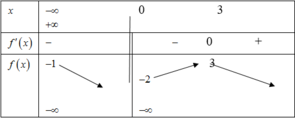
Dựa vào bảng biến thiên nhận thấy hàm số đồng biến trên các khoảng - ∞ ; - 1 và (-1;1)
Vì vậy khẳng đinh C là sai. Chọn C.