Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt ![]() khi đó yêu cầu bài toán trở thành phương trình
khi đó yêu cầu bài toán trở thành phương trình
![]() có nghiệm
t
∈
(
0
;
1
]
Có
có nghiệm
t
∈
(
0
;
1
]
Có
![]()
Do đó
![]()
![]()
![]()
Vậy ![]()
Tổng các phần tử của tập S bằng -10.
Chọn đáp án D.

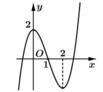
Đặt t = sin x ∈ ( 0 ; 1 ] , ∀ x ∈ ( 0 ; π ) Phương trình trở thành: f(t)=m(1)
Ta cần tìm m để (1) có nghiệm thuộc khoảng ( 0 ; 1 ] ⇔ - 4 ≤ m < - 2
Chọn đáp án C.

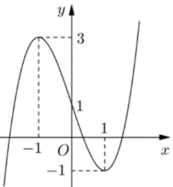
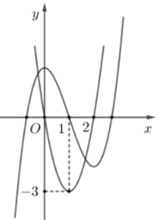
Để phương trình f(cosx) = m có 3 nghiệm x phân biệt thuộc khoảng ( 0 ; 3 π 2 ] thì phương trình f(cosx) = m phải có hai nghiệm cosx phân biệt, trong đó có 1 nghiệm thuộc (-1;0] và một nghiệm thuộc (0;1)
Dựa vào đồ thị, suy ra m ∈ (0;2)
Chọn B.

![]()
![]()
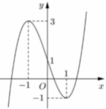
Do đó phương trình f[f(sinx)] = m có nghiệm thuộc khoảng 0 ; π khi và chỉ khi phương trình
f(t) = m có nghiệm thuộc nửa khoảng [-1;1]
Dựa vào đồ thị, suy ra ![]()
Chọn C.

Đặt t=2sinx+1 với
![]()
![]()
![]()
Phương trình trở thành: f(t)=m có nghiệm ![]()
Chọn đáp án A.

Ta có ![]()
![]()
Quan sát đồ thị có 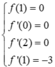
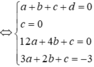

![]()
Đặt ![]() phương trình trở thành:
phương trình trở thành:
![]()
![]()
![]()
Khi đó ![]()
Phương trình này có 3 nghiệm phân biệt
![]()
Tổng các phần tử củaS bằng 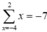
Chọn đáp án C.
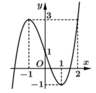





Đặt t = sinx do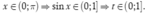
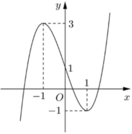
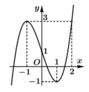
● Gọi ∆ 1 là đường thẳng qua điểm (1;-1) và song song với đường thẳng y = 3x nên có phương trình y = 3x - 4
● Gọi ∆ 2 là đường thẳng qua điểm (0;1) và song song với đường thẳng y = 3x nên có phương trình y = 3x+1
Do đó phương trình f sin x = 3 sin x + m có nghiệm thuộc khoảng 0 ; π khi và chỉ khi phương trình f(t) = 3t + m có nghiệm thuộc nửa khoảng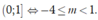 Chọn A.
Chọn A.