Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
khảo sát
TXD mọi x
y' =3x^2 -6x =3x(x-2)
y' =0 => x= 0 hoặc x=2
y'' =6x-6
y''(0) =-6 <0 hàm đạt cực đại tại x=0
y''(2) =6 >0 hàm đạt cực tiểu tại x =2
y'' =0 => x=1 hàm có điểm uốn tại x=1
hàm đi từ - vc--> +vc đi góc (III) lên (IV)
Vẽ đồ thị
Các điểm quan trọng
cực đại A(0,0)
cực tiểu B(2,-4)
uốn C(1,-2)
Các điểm phụ trọng
giao với trục hoành E(0,0); \(F\left(3;0\right)\)
Giao với trục tung: \(A\left(0,0\right)\)
Đồ thị

b)
nhìn vào đồ thị số y=x^3 -3x^2
Hàm số x^3 -3x^2 -m có 3 nghiệm phân biệt
khi 0<m<-4

Xét
\(y'=4x^3-4\left(m-1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=m-1\end{cases}}\)
TH1:
\(m-1\le0\) thì hàm số đồng biến trên R
TH2: \(m-1>0\Rightarrow\orbr{\begin{cases}x=\sqrt{m-1}\\x=-\sqrt{m-1}\end{cases}}\)
Khi đó khoảng đồng biến của hàm số là \(\left(-\infty,-\sqrt{m-1}\right)\text{ và }\left(0,\sqrt{m-1}\right)\)
Muốn hàm số đồng biến trên (1,3) thì \(\left(1,3\right)\subset\left(0,\sqrt{m-1}\right)\Leftrightarrow3\le\sqrt{m-1}\Leftrightarrow m\ge10\)
Vậy \(\orbr{\begin{cases}m\le1\\m\ge10\end{cases}}\)

Đáp án D
Ta có ![]()
![]()
![]() . Số nghiệm của phương trình
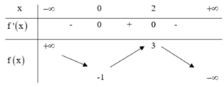
. Số nghiệm của phương trình ![]() chính là số giao điểm của đồ thị hàm số H và đường thẳng
chính là số giao điểm của đồ thị hàm số H và đường thẳng ![]() .
.
Dựa vào bảng biến thiên ta thấy ![]() có ba nghiệm phân biệt khi:
có ba nghiệm phân biệt khi:
![]()
![]()
![]() .
.










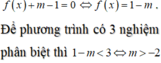
Đáp án C
Phương pháp:
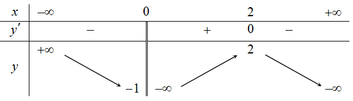
Số nghiệm của phương trình f(x) = m bằng số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
Cách giải:
Số nghiệm của phương trình f(x) = m(*) bằng số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
⇒ Để (*) có 3 nghiệm thực phân biệt thì m ∈ (-1;3)