DT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
16 tháng 3 2019
Chọn C
Ta có y ' = 4 − 1 2 x
y ' ( x ) = 0 ⇔ 4 − 1 2 x = 0
⇔ 4 = 1 2 x ⇔ 8 x = 1 ⇔ x = 1 8 ⇔ x = 1 64
13 tháng 8 2023
\(y'=12x^3-6x-6\)
\(=6\left(2x^3-x-1\right)=6\left(x-1\right)\left(2x^2+2x+1\right)\)
\(\Rightarrow\) Nghiệm của pt \(y'=0\) là \(x=1\)
HP
5 tháng 10 2021
1.
Hàm số xác định khi: \(1-2sinx\ne0\Leftrightarrow sinx\ne\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x\ne\dfrac{\pi}{6}+k2\pi\\x\ne\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
17 tháng 5 2021
Điều kiện: \(x\ne1\)
a) Xét phương trình: \(\frac{x^2-2mx+3m-2}{x-1}=0\Leftrightarrow x^2-2mx+3m-2=0\)\(\left(x-1\ne0\right)\)
Pt có hai nghiệm phân biệt \(\Leftrightarrow\Delta'>0\Leftrightarrow m^2-3m+2>0\Leftrightarrow\orbr{\begin{cases}m>2\\m< 1\end{cases}}\)
Khi đó \(\hept{\begin{cases}x_1=m-\sqrt{m^2-3m+2}\\x_2=m+\sqrt{m^2-3m+2}\end{cases}}\)
+) \(x_1,x_2\ne1\Leftrightarrow\hept{\begin{cases}m-\sqrt{m^2-3m+2}\ne1\\m+\sqrt{m^2-3m+2}\ne1\end{cases}\Leftrightarrow m\ne1}\)
+) Tiếp tuyến của đồ thị tại hai giao điểm với trục Ox vuông góc với nhau
\(\Leftrightarrow\hept{\begin{cases}y'\left(x_1\right)=-1\left(1\right)\\y'\left(x_2\right)=1\left(2\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow\frac{\left(2x_1-2m\right)\left(x_1-1\right)-\left(x_1^2-2mx_1+3m-2\right)}{\left(x_1-1\right)^2}=-1\)
\(\Leftrightarrow\frac{m-1}{\left(x_1-1\right)^2}=2\Rightarrow m-1=2\left(m-\sqrt{m^2-3m+2}-1\right)^2\)
\(\Leftrightarrow\left(m-1\right)\left[1-2\left(2m-3-2\sqrt{m^2-3m+2}\right)\right]=0\)
\(\Leftrightarrow4\sqrt{m^2-3m+2}=4m-7\Leftrightarrow\hept{\begin{cases}m\ge\frac{7}{4}\\m=\frac{17}{8}\end{cases}}\Leftrightarrow m=\frac{17}{8}\)(t/m m>2 v m<1)
Giải (2) cho ra \(m=1\)(loại). Vậy m cần tìm là \(m=\frac{17}{8}.\)
CM
30 tháng 4 2019
Chọn B.
y ' = cot 2 x 4 ' = 2 cot x 4 cot x 4 ' = 1 2 cot x 4 1 + cot 2 x 4
y ' = 0 ⇔ 1 2 cot x 4 1 + cot 2 x 4 = 0
⇔ cot x 4 = 0 ⇔ x 4 = π 2 + k π ⇔ x = 2 π + k 4 π , k ∈ ℤ
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 1 2022
Xét pt \(\left|x^2-2\left|x\right|+m\right|=1\Leftrightarrow\left|\left(\left|x\right|-1\right)^2+m-1\right|=1\) (1)
Đặt \(\left(\left|x\right|-1\right)^2=t\ge0\) (2)
Ta thấy:
- Với \(\left[{}\begin{matrix}t=0\\t>1\end{matrix}\right.\) \(\Rightarrow\) (2) có 2 nghiệm
- Với \(t=3\Rightarrow\) (2) có 3 nghiệm
- Với \(0< t< 1\Rightarrow\) (2) có 4 nghiệm
- Với \(t< 0\Rightarrow\) (2) vô nghiệm
Xét pt: \(\left|t+m-1\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}t+m-1=1\\t+m-1=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}t=2-m\\t=-m\end{matrix}\right.\) luôn có 2 nghiệm
\(\Rightarrow\) (1) có 2 nghiệm khi
TH1: \(\left[{}\begin{matrix}-m< 0\\2-m=0\end{matrix}\right.\) \(\Rightarrow m=2\) (TH này pt có 2 nghiệm, nhưng đó là 2 nghiệm kép)
TH2: \(\left[{}\begin{matrix}-m< 0\\2-m>1\end{matrix}\right.\) \(\Rightarrow0< m< 1\)
CM
6 tháng 7 2019
Chọn A.
y' = (m + 1)cosx – msinx – ( m + 2)
Phương trình y’ = 0 ⇔ (m + 1)cosx – msinx = (m + 2)
Điều kiện phương trình có nghiệm là a2 + b2 ≥ c2
⇔ (m + 1)2 + m2 ≥ (m + 2)2 ⇔ m2 – 2m – 3 ≥ 0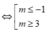 
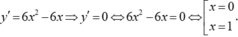
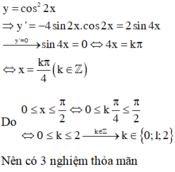
Lời giải:
Ta có:
\(y'=(e^x+e^{-x})'=e^x-e^{-x}=e^x-\frac{1}{e^x}\)
\(y'=0\Leftrightarrow e^x-\frac{1}{e^x}=0\Leftrightarrow e^{2x}-1=0\)
\(\Leftrightarrow e^{2x}=1\Leftrightarrow 2x=0\Leftrightarrow x=0\)