Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Tập xác định: D=R Ta có y = 3 a x 2 + 2 b x + c
Do đồ thị (C) có hai điểm cực trị nên ta có phương trình y '=0 có hai nghiệm phân biệt hay là phương trình 3 a x 2 + 2 b x + c = 0 có hai nghiệm phân biệt xi, xj và hai nghiệm này cũng chính là hoành độ của hai điểm cực trị của đồ thị (C). theo vi-ét ta có x i + x j = - 2 b 3 a .
Suy ra hoành độ giao điểm nối hai điểm cực trị là
x 0 = x i + x j 2 = 1 3 ⇔ - 2 b 3 a = 2 3 ⇔ b = - a .
Mặt khác do giả thiết ta có phương trình a x 3 + b x 2 + c x + d = 0 có ba nghiệm phân biệt x1, x2, x3 nên theo vi-ét ta có x 1 + x 2 + x 3 = - b a = a a = 1 .
Ta có:
3 x 1 + 4 x 2 + 5 x 3 2 = 44 x 1 x 2 + x 2 x 3 + x 3 x 1 ⇔ 9 x 1 2 + 16 x 2 2 + 25 x 3 2 = 20 x 1 x 2 + 4 x 2 x 3 + 14 x 3 x 1
⇔ 20 3 x 1 2 + 40 3 x 2 2 + x 2 2 + 4 x 3 2 + 7 3 x 1 2 + 21 x 3 2 = 20 x 1 x 2 + 4 x 2 x 3 + 14 x 3 x 1
Áp dụng bất đẳng thức Cauchuy ta có:
- 5 3 4 x 1 2 + 9 x 2 2 ≥ 5 3 . 2 4 x 1 1 . 9 x 2 2 = 20 x 1 x 2 (1).
- x 2 2 + 4 x 3 2 ≥ 2 x 2 2 . 4 x 3 2 = 4 x 1 x 2 (2).
- 7 12 4 x 1 2 + 36 x 3 2 ≥ 7 12 . 2 4 x 1 2 . 36 x 3 2 = 14 x 3 x 1 (3).
Lấy (1) + (2) + (3) vế theo vế ta có: 9 x 1 2 + 16 x 2 2 + 25 x 3 2 ≥ 20 x 1 x 2 + 4 x 2 x 3 + 14 x 3 x 1 .
Dấu đẳng thức xảy ra khi và chỉ khi:
4 x 1 2 = 9 x 2 2 x 2 2 = 4 x 3 2 4 x 1 2 = 36 x 3 2 x 1 + x 2 + x 3 = 1 ⇔ x 1 = 3 2 x 2 x 2 = 2 x 3 x 3 = 1 3 x 1 x 1 + x 2 + x 3 = 1 ⇔ x 1 =...

Đáp án D
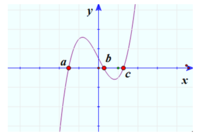
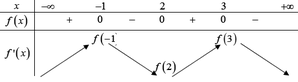
Trên khoảng ( a ; b ) và ( c ; + ∞ ) hàm số đồng biến vì y'>0 đồ thị nằm hoàn toàn trên trục Ox
Hàm số nghịch biến trên các khoảng ( - ∞ ; a ) và (b;c) vì y'<0
Suy ra x=b là điểm cực đại mà y(b) <0 do đó trục hoành cắt đồ thị tại hai điểm phân biệt. Với d<0 ta có

Đáp án D
y ' = 4 a x 3 + 2 b x , y ' 1 = - 4 a - 2 b
Phương trình tiếp tuyến tại A là: d: y=(-4a-2b)(x+1)
Xét phương trình tương giao: a x 4 + b x 2 + c = ( - 4 a - 2 b ) ( x + 1 )
Phương trình có 2 nghiệm x=0,x=2 => 4 a + 2 b + c = 0 28 a + 10 b + c = 0 ( 1 )
∫ 0 2 - 4 a - 2 b x + 1 - a x 4 - b x 2 - c d x = - 2 a - b x 2 + - 4 a - 2 b x - a x 5 5 - b x 3 3 - c x 2 0 = - 112 5 a - 32 3 b - 2 c = 28 5 2 1 , 2 ⇒ a = 1 b = - 3 ⇒ y = x 4 - 3 x 2 + 2 , d : y = 2 x + 2 c = 2 ⇒ S = ∫ - 1 0 x 4 - 3 x 2 + 2 d x = x 5 5 - x 3 - x 2 0 - 1 = 1 5

Đáp án D

∫ 0 2 [ ( − 4 a − 2 b ) ( x + 1 ) − ax 4 − b x 2 − c ] d x = [ ( − 2 a − b ) x 2 + ( − 4 a − 2 b ) x − ax 5 5 − b x 3 3 − c x ] 2 0 = − 112 5 a − 32 3 b − 2 c = 28 5 ( 2 ) ( 1 ) , ( 2 ) ⇒ a = 1 b = − 3 c = 2 ⇒ y = x 4 − 3 x 2 + 2 , d : y = 2 x + 2 ⇒ S = ∫ − 1 0 ( x 4 − 3 x 2 + 2 ) d x = x 5 5 − x 3 − x 2 0 − 1 = 1 5

Đáp án D.

Ta có y ' = 4 a x 3 + 2 b x → y ' − 1 = − 4 a − 2 b . Phương trình tiếp tuyến của (C) tại điểm A − 1 ; 0 là đường thẳng
d : y = y ' − 1 . x + 1 ⇔ y = − 4 a − 2 b x − 4 a − 2 b
Phương trình hoành độ giao điểm của đường thẳng d và đồ thị (C) là:
a x 4 + b x 2 + c = − 4 a + 2 b x − 4 a − 2 b ⇔ a x 4 + b x 2 + 4 a + 2 b x + 4 a + 2 b + c = 0 (*)
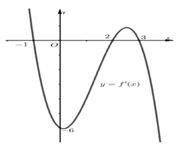
Quan sát đồ thị, ta thấy đường thẳng d cắt đồ thị tại hai điểm có hoành độ x = 0, x = 2 nên phương trình (*) có hai nghiệm x = 0, x = 2 .
Suy ra
4 a + 2 b + c = 0 16 a + 4 b + 2 4 a + 2 b + 4 a + 2 b + c = 0 ⇔ 4 a + 2 b + c = 0 28 a + 10 b + c = 0 (1)
Diện tích hình phẳng giới hạn bởi đường thẳng d, đồ thị (C) và hai đường thẳng x = 0, x = 2 là
S = ∫ 0 2 − 4 a − 2 b x − 4 a − 2 b − a x 4 + b x 2 + c d x = 28 5
⇔ ∫ 0 2 − 4 a − 2 b x − 4 a − 2 b − a x 4 − b x 2 − c d x = 28 5
⇔ − a 5 x 5 − b 3 x 3 − 2 a + b x 2 − 4 a + 2 b + c x 0 2 = 28 5
⇔ − 32 5 a − 8 b 3 − 4 2 a + b − 2 4 a + 2 b + c = − 28 5 ⇔ 112 5 a...

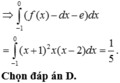


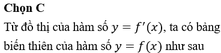






Chọn đáp án C
Ta có
⇔ x = - b 3 a
Đồ thị (C) có hai điểm cực trị thì trung điểm của đoạn thẳng nối hai điểm cực trị đó chính là điểm uốn U của đồ thị và hoành độ của điểm U là nghiệm của phương trình y'' = 0. Từ giả thiết ta có
Lại có phương trình hoành độ giao điểm a x 3 + b x 2 + c x + d = 0 có ba nghiệm dương phân biệt x 1 , x 2 , x 3 .
Theo định lý Vi-ét ta có
Từ giả thiết
Áp dụng bất đẳng thức Cau-chy cho các số dương ta có:
; dấu “=” xảy ra khi 2 x 1 = 3 x 2
; dấu “=” xảy ra khi 2 x 1 = 6 x 3
; dấu “=” xảy ra khi x 2 = 2 x 3
Cộng theo vế của ba bất đẳng thức trên ta đươc
Dấu “=” xảy ra khi
Vậy S = x 1 + x 2 2 + x 3 2 = 133 216