Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔ 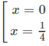
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )
b) TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 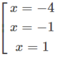
Bảng biến thiên:
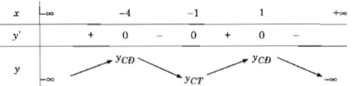
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
c) TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng ( - ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 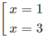
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)

Đáp án: D.
Vì x 2 + x + 4 > 0 với mọi x nên phương trình (x − 3)( x 2 + x + 4) = 0 chỉ có một nghiệm là x = 3. Do đó, đồ thị của hàm số đã cho chỉ có một giao điểm với trục hoành.

Đáp án: D.
Vì x 2 + x + 4 > 0 với mọi x nên phương trình (x − 3)( x 2 + x + 4) = 0 chỉ có một nghiệm là x = 3. Do đó, đồ thị của hàm số đã cho chỉ có một giao điểm với trục hoành.

Đáp án: D.
Hàm số y = x 4 - 5 x 2 + 4 xác định trên R.
y' = 4 x 3 - 10x = 2x(2 x 5 - 5);
y' = 0 khi

y'' = 12 x 2 - 10
Vì y''(0) = -10 < 0,

nên hàm số chỉ có một cực đại (tại x = 0)
Cách khác: Vì a > 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = a x 4 + b x 2 + c có một cực đại

Đáp án: D.
Hàm số y = x 4 - 5 x 2 + 4 xác định trên R.
y' = 4 x 3 - 10x = 2x(2 x 2 - 5);
y' = 0 khi
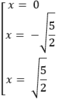
y'' = 12 x 2 - 10
Vì y''(0) = -10 < 0,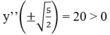
nên hàm số chỉ có một cực đại (tại x = 0)
Cách khác: Vì a > 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = a x 4 + b x 2 + c có một cực đại

Đáp án: B.
Vì a < 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = a x 4 + b x 2 + c có hai cực đại, một cực tiểu.
Ở đây y' = -4 x 3 + 8x; y' = 0 ⇔ -4x( x 2 - 2) = 0
⇔ 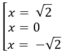

Đáp án: B.
Vì a < 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = a x 4 + b x 2 + c có hai cực đại, một cực tiểu.
Ở đây y' = -4 x 3 + 8x; y' = 0 ⇔ -4x( x 2 - 2) = 0
⇔ 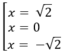
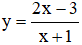
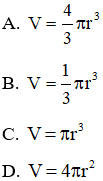
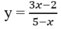 là y = -3;
là y = -3;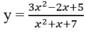
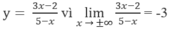
+ Ta có đạo hàm : y’ = 3.( 4- x2)2. ( 4-x2)’= -6x( 4-x2)2
+ đạo hàm cấp 2:
y’’= -6( 4-x2)2- 6x.2( 4-x2). ( -2x) = - 6.( 4-x2) .[ ( 4-x2) + 2x. ( -2x)]
= -6( 4-x2) .[ 4-x2- 4x2] = - 6( 4-x2). ( 4- 5x2)
Do đó; y’ (1) = -6( 4- 12).( 4- 5.12) = -6. 3.( -1)= 18
Chọn A.