
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) Ta có \(y'=4x^3-4x;y\left(-2\right)=8;y'\left(-2\right)=-24\)
Phương trình tiếp tuyến phải tìm là :
\(y-y\left(-2\right)=y'\left(-1\right)\left(x+2\right)\)
\(\Leftrightarrow y-8=-24\left(x+2\right)\Leftrightarrow y=-24x-10\)

a) Hàm số y= 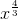
Tập xác định: (0; +∞).
Sự biến thiên: 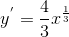 > 0, ∀x ∈ (0; +∞) nên hàm số luôn luôn đồng biến.
> 0, ∀x ∈ (0; +∞) nên hàm số luôn luôn đồng biến.
Giới hạn đặc biệt: 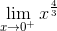 = 0,
= 0, 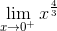 = +∞, đồ thị hàm số có tiệm cận.
= +∞, đồ thị hàm số có tiệm cận.
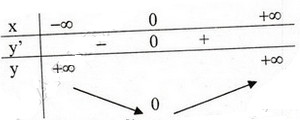
Bảng biến thiên
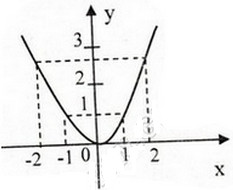
Đồ thị( hình bên). Đồ thị hàm số qua (1;1), (2;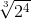 ).
).
b) y= 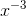 .
.
Tập xác định: ℝ \{0}.
Sự biến thiên: 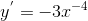 < 0, ∀xj# 0, hàm nghich biến trong hai khoảng (-∞;0) và (0; +∞).
< 0, ∀xj# 0, hàm nghich biến trong hai khoảng (-∞;0) và (0; +∞).
Giới hạn đặc biệt: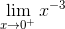 = +∞,
= +∞, 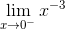 = -∞,
= -∞, 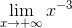 = 0,
= 0, 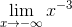 = 0; đồ thị hàm số nhận trục tung làm tiệm cận đứng, trục hoành làm tiệm cận ngang.
= 0; đồ thị hàm số nhận trục tung làm tiệm cận đứng, trục hoành làm tiệm cận ngang.
Bảng biến thiên
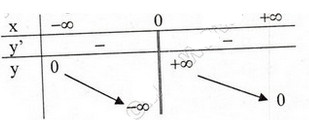
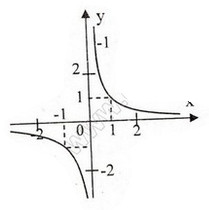
Đồ thị ( hình dưới). Đồ thị qua (-1;-1), (1;1), (2;  ), ( -2;
), ( -2; 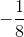 ). Hàm số đồ thị đã cho là hàm số lẻ nên đối xứng qua gốc tọ độ.
). Hàm số đồ thị đã cho là hàm số lẻ nên đối xứng qua gốc tọ độ.

\(y=-x^4+2\left(m+1\right)x^2+m+1\left(C_m\right)\)
\(y'=-4x^2+4\left(m+1\right)x=-4x\left(x^2-m-1\right)\)
Xét \(y'=0\Leftrightarrow-4x\left(x^2-m-1\right)=0\) \(\Leftrightarrow\begin{cases}x=0\\x^2=m+1\left(1\right)\end{cases}\)
Hàm số có 3 điểm cực trị khi và chỉ khi phương trình \(y'=0\) có 3 nghiệm phân biệt \(\Leftrightarrow\) phương trình (1) có 2 nghiệm phân biệt khác 0
\(\Leftrightarrow m+1>0\Leftrightarrow m>-1\) (*)
Với điều kiện (*) phương trình y' = 0 có 3 nghiệm phân biệt \(x,x=\pm\sqrt{m+1}\) và có 3 điểm cực trị của đồ thị \(C_m\) là \(A\left(0;m+1\right);B\left(-\sqrt{m+1;}-\left(m+1\right)^2+m+1;\right);C\left(\sqrt{m+1};-\left(m+1\right)^2+m+1\right)\)
3 điểm cực trị tạo thành 1 tam giác đều :
\(\Leftrightarrow AB=AC=CB\Leftrightarrow AB^2=AC^2=CB^2\)
\(\Leftrightarrow\begin{cases}AB^2=AC^2\\AB^2=BC^2\end{cases}\)\(\Leftrightarrow\begin{cases}m+1+\left(m+1\right)^4=m+1+\left(m+1\right)^4\\m+1+\left(m+1\right)^4=4\left(m+1\right)\end{cases}\)
\(\Leftrightarrow m=\sqrt[3]{3}-1\)







Ta có:
Trước hết, ta vẽ đồ thị (C) của hàm số
TXĐ: D = R \ {−3/2}.
Vì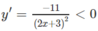
với mọi nên hàm số nghịch biến trên các khoảng
Bảng biến thiên:
Tiệm cận đứng x = −3/2
Tiệm cận ngang y = −1/2
Đồ thị (C) đi qua các điểm (−2;−6),(−1;5),(0;4/3),(4;0)
Để vẽ đồ thị (C’) của hàm số , ta giữ nguyên phần đồ thị (C) nằm phía trên trục hoành và lấy đối xứng phần đồ thị (C) nằm phía dưới trục hoành qua trục hoành.