
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm

y’ = 3x2 – 2mx – 2 , ∆’ = m2 + 6 > 0 nên y’ = 0 có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
Vậy hàm số luôn có một cực đại và một cực tiểu.

Ta có : \(y'=4x^3+12mx^2+6\left(m+1\right)x=2x\left(2x^2+6mx+3\left(m+1\right)\right)\)
\(\Rightarrow y'=0\Leftrightarrow x=0\) hoặc
\(\Leftrightarrow f\left(x\right)=2x^2+6mx+3m+3=0\)
a) Hàm số có 3 cực trị khi và chỉ khi \(f\left(x\right)\) có 2 nghiệm phân biệt khác 0
\(\Leftrightarrow\begin{cases}\Delta'=3\left(3m^2-2m-2\right)>0\\f\left(0\right)\ne0\end{cases}\)\(\Leftrightarrow\begin{cases}m< \frac{1-\sqrt{7}}{3}\cup m>\frac{1+\sqrt{7}}{3}\\m\ne-1\end{cases}\)
b) Hàm số chỉ có cực tiểu mà không có cực đại
\(\Leftrightarrow\) hàm số không có 3 cực trị \(\Leftrightarrow\frac{1-\sqrt{7}}{3}\le m\le\frac{1+\sqrt{7}}{3}\)

Hàm số có cực địa và cực tiểu <=> phương trình y'(x) = 0 có hai nghiệm phân biệt :
\(\Leftrightarrow3\left(m+2\right)x^2+6x+m=0\) có 2 nghiệm phân biệt
\(\Leftrightarrow\begin{cases}m+2\ne0\\\Delta'=-3m^2-6m+9>0\end{cases}\)\(\Leftrightarrow\begin{cases}m\ne-2\\m^2+2m-3< 0\end{cases}\) \(\Leftrightarrow-3< m\ne-2< 1\)

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

Xét \(f'\left(x\right)=4x^3+3mx^2+2mx+m=0\Leftrightarrow m\left(3x^2+2x+1\right)=-4x^3\)
\(\Leftrightarrow\frac{-4x^3}{3x^2+2x+1}\)
Xét hàm số : \(g\left(x\right)=\frac{-4x^3}{3x^2+2x+1}\) có tập xác định : \(D_g=!\)
\(g'\left(x\right)=\frac{-4x^2\left(3x^2+2x+1\right)}{\left(3x^2+2x+1\right)^2}=\frac{-4x^2\left[2\left(x+1\right)^2+x^2+1\right]}{\left(3x^2+2x+1\right)^2}\le0\) với mọi \(x\in!\)
\(\lim\limits g\left(x\right)_{x\rightarrow\infty}=\lim\limits_{x\rightarrow\infty}\frac{-4x}{3+\frac{2}{x}+\frac{1}{x^2}}=\infty\)
Nghiệm của phương trình \(f'\left(x\right)=0\) cũng là giao điểm của đường thẳng y=m với đồ thị y = g(x)
Lập bảng biến thiên ta có đường thẳng y=m cắt y =g(x) tại đúng 1 điểm
\(\Rightarrow f'\left(x\right)=0\)
có đúng 1 nghiệm
Vậy hàm số y=f(x) không thể đồng thời có cực đại và cực tiểu

\(f'\left(x\right)=6\left(x^2+\left(m-1\right)x+m\left(1-2m\right)\right)\)
\(f'\left(x\right)=0\Leftrightarrow g\left(x\right)=x^2+\left(m-1\right)x+m\left(1-2m\right)=0\)
Hàm số có cực đại, cực tiểu <=> \(f'\left(x\right)=0\) hay \(g\left(x\right)=0\) có 2 nghiệm phân biệt \(\Leftrightarrow\Delta_g=\left(m-1\right)^2-4m\left(1-2m\right)=\left(3m-1\right)^2>0\Leftrightarrow m\ne\frac{1}{3}\)
Ta có \(f\left(x\right)=g\left(x\right)\left[2x+\left(m+1\right)\right]-\left(3m-1\right)^2x+m\left(m-1\right)\left(1-2m\right)\)
Với \(m\ne\frac{1}{3}\) thì \(g\left(x\right)=0\) có 2 nghiệm phân biệt \(x_1;x_2\) và hàm số đạt cực trị tại \(x_1;x_2\)
do \(\begin{cases}g\left(x_1\right)=0\\g\left(x_2\right)=0\end{cases}\) suy ra đường thẳng qua cực đại, cực tiểu là
\(\Delta:y=-\left(3m-1\right)^2x+m\left(m-1\right)\left(1-2m\right)\)
Ta có cực địa, cực tiểu nằm trên đường thẳng \(y=-4x\)
\(\Leftrightarrow\begin{cases}-\left(3m-1\right)^2=-4\\m\left(m-1\right)\left(1-2m\right)=0\end{cases}\)\(\Leftrightarrow\begin{cases}\left|3m-1\right|=2\\m\in\left\{0;1;\frac{1}{2}\right\}\end{cases}\) \(\Leftrightarrow m=1\)

a) Xét phương trình : \(f'\left(x\right)=2x^2+2\left(\cos a-3\sin a\right)x-8\left(1+\cos2a\right)=0\)
Ta có : \(\Delta'=\left(\cos a-3\sin a\right)^2+16\left(1+\cos2a\right)=\left(\cos a-3\sin a\right)^2+32\cos^2\), \(a\ge0\) với mọi a
Nếu \(\Delta'=0\Leftrightarrow\cos a-3\sin a=\cos a=0\Leftrightarrow\sin a=\cos a\Rightarrow\sin^2a+\cos^2a=0\) (Vô lí)
Vậy \(\Delta'>0\)
với mọi a \(\Rightarrow f'\left(x\right)=0\)
có 2 nghiệm phân biệt \(x_1,x_2\) và hàm số có cực đại, cực tiểu
b) Theo Viet ta có \(x_1+x_2=3\sin a-\cos a\)
\(x_1x_2=-4\left(1+\cos2a\right)\)
\(x^2_1+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(3\sin a-\cos a\right)^2+8\left(1+\cos2a\right)=9+8\cos^2a-6\sin a\cos a\)
\(=9+9\left(\sin^2a+\cos^2a\right)-\left(3\sin a+\cos a\right)^2=18-\left(3\sin a+\cos2a\right)\le18\)

Tập xác định \(D=R\backslash\left\{m\right\}\)
Ta có : \(y'=\frac{x^2-2mx+m^2-1}{\left(x-m\right)^2}\Rightarrow y'=0\Leftrightarrow x^2-2mx+m^2-1=0\left(1\right)\left(x\ne m\right)\)
Ta thấy phương trình (1) luôn có 2 nghiệm phân biệt khác m và y' đổi dấu qua 2 nghiệm đó. Vậy hàm số luôn có cực trị với mọi giá trị của m

Đáp án: B.
Vì a < 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = a x 4 + b x 2 + c có hai cực đại, một cực tiểu.
Ở đây y' = -4 x 3 + 8x; y' = 0 ⇔ -4x( x 2 - 2) = 0
⇔ 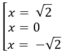
Ta có y ' = - 12 x 3 - 4 x
Xét y'=0 => x = 0
Hàm số chỉ có một cực đại tại x = 0. Chọn đáp án C.