
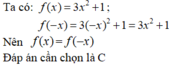
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
nếu x1<x2=>2018.x1-3<2018.x2
=>f(x1)<f(x2)
Bài 2:
nếu x dương=>100x2+2 dương
nếu x âm=>100x2+2 dương vì x2 luôn dương
=>f(x)=f(-x)
Bài 3:
nếu x1<x2=>-2019x1+1<2019x2+1
=>f(x1)<f(x2)

Lời giải:
Ta có:
\(f(x)=-5x\Rightarrow \left\{\begin{matrix} f(x_1)=-5x_1\\ f(x_2)=-5x_2\end{matrix}\right.\)
\(\Rightarrow f(x_1)-f(x_2)=-5x_1-(-5)x_2=-5(x_1-x_2)=5(x_2-x_1)\)
Do \(x_2> x_1\Rightarrow 5(x_2-x_1)>0\Leftrightarrow f(x_1)-f(x_2)>0 \)
\(\Leftrightarrow f(x_1)> f(x_2)\) (đpcm)
b)
\(\left\{\begin{matrix} f(x_1)=-5x_1\\ f(x_2)=-5x_2\rightarrow 4f(x_2)=-20x_2\end{matrix}\right.\)
\(\Rightarrow f(x_1)+4f(x_2)=-5x_1+(-20)x_2=-5x_1-20x_2\) (1)
Lại có:
\(f(x)=-5x\rightarrow f(x_1+4x_2)=-5(x_1+4x_2)=-5x_1-20x_2\) (2)
Từ (1),(2) suy ra \(f(x_1+4x_2)=f(x_1)+4f(x_2)\)
c)
\(f(x)=-5x\Rightarrow -f(x)=-(-5x)=5x\)
\(f(x)=-5x\Rightarrow f(-x)=-5(-x)=5x\)
Do đó: \(-f(x)=f(-x)\)

a) Với x1 = x2 = 1
\(\Rightarrow f\left(1\right)=f\left(1.1\right)\)
\(\Rightarrow f\left(1\right)=f\left(1\right).f\left(1\right)\)
\(\Rightarrow f\left(1\right).f\left(1\right)-f\left(1\right)=0\)
\(\Rightarrow f\left(1\right).\left[f\left(1\right)-1\right]=0\)
\(\Rightarrow\orbr{\begin{cases}f\left(1\right)=0\\f\left(1\right)-1=0\end{cases}}\)
Mà \(f\left(x\right)\ne0\) ( với mọi \(x\in R\) \(;\) \(x\ne0\) )
\(\Rightarrow f\left(1\right)\ne0\)
\(\Rightarrow f\left(1\right)-1=0\)
\(\Rightarrow f\left(1\right)=1\)
b) Ta có : \(f\left(\frac{1}{x}\right).f\left(x\right)=f\left(\frac{1}{x}.x\right)\)
\(\Rightarrow f\left(\frac{1}{x}\right).f\left(x\right)=f\left(1\right)=1\)
\(\Rightarrow f\left(\frac{1}{x}\right).f\left(x\right)=1\)
\(\Rightarrow f\left(\frac{1}{x}\right)=\frac{1}{f\left(x\right)}\)
\(\Rightarrow f\left(x^{-1}\right)=\left[f\left(x\right)\right]^{-1}\)