Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: Thay x=1 và y=1 vào hàm số, ta được:
y=2x1-3=-1<>1
Vậy: Điểm M ko thuộc đồ thị
b: Hàm số đồng biến vì a=2>0

Lời giải:
a. Vì $(d)$ đi qua $M(3;1)$ nên:
$y_M=(2-a)x_M+a$
$\Leftrightarrow 1=(2-a).3+a\Rightarrow a=2,5$
Khi đó: $y=(2-2,5)x+2,5=-0,5x+2,5$
Vì $-0,5<0$ nên hàm nghịch biến trên R.
b.
$y_A=3$
$-0,5x_A+2,5=-0,5.(-1)+2,5=3$
$\Rightarrow y_A=-0,5x_A+2,5$ nên điểm $A\in (d)$
c. Gọi PTĐT $(d')$ là: $y=mx+n$ với $m,n$ là số thực
$(d')\parallel (d)$ nên $m=-0,5$
$M(3;1), N(-1,5)\Rightarrow$ tọa độ trung điểm $I$ của $MN$ là:
$(\frac{3-1}{2}; \frac{1+5}{2})=(1,3)$
$(d')$ đi qua $(1,3)$ nên:
$3=m.1+n\Rightarrow m+n=3\Rightarrow n=3-m=3-(-0,5)=3,5$
Vậy PTĐT $(d')$ là: $y=-0,5x+3,5$

1: (D): y=(m-2)x+1
(D'): \(y=m^2x-2x+m=x\left(m^2-2\right)+m\)
Để (D) là hàm số bậc nhất thì m-2<>0
=>m<>2
Để (D): y=(m-2)x+1 đồng biến trên R thì m-2>0
=>m>2
Để (D): y=(m-2)x+1 nghịch biến trên R thì m-2<0
=>m<2
2: Để (D)//(D') thì \(\left\{{}\begin{matrix}m^2-2=m-2\\m< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2-m=0\\m< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\m< >1\end{matrix}\right.\)
=>m=0
3:
a: Khi m=0 thì (D): y=(0-2)x+1=-x+1
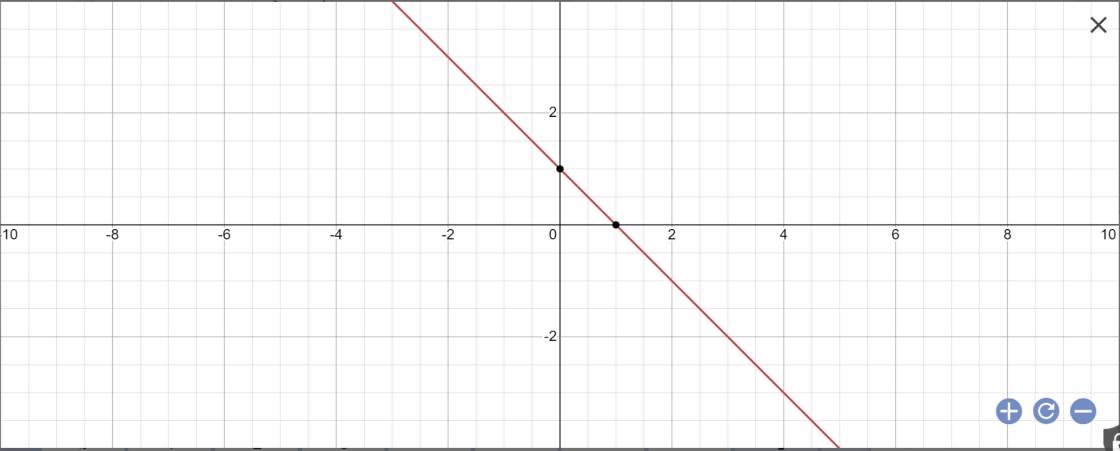
b: Gọi \(\alpha\) là góc tạo bởi (D) với trục Ox
Ta có: a=-1
nên \(tan\left(180^0-\alpha\right)=-1\)
=>\(180-\alpha=135^0\)
=>\(\alpha=45^0\)
4:
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}2x-8=-x+1\\y=2x-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=9\\y=2x-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\cdot3-8=-2\end{matrix}\right.\)
Thay x=3 và y=-2 vào (D), ta được:
\(3\left(m-2\right)+1=-2\)
=>3(m-2)=-3
=>m-2=-1
=>m=1
5: Để (D) cắt (D') tại một điểm trên trục hoành thì
\(\left\{{}\begin{matrix}m-2< >m^2-2\\-\dfrac{1}{m-2}=\dfrac{-m}{m^2-2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2-m\ne0\\\dfrac{1}{m-2}=\dfrac{m}{m^2-2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-1\right)\ne0\\m^2-2=m^2-2m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\notin\left\{0;1\right\}\\-2m=-2\end{matrix}\right.\)
=>\(m\in\varnothing\)
6: (D): y=(m-2)x+1
=>y=mx-2x+1
Điểm mà (D) luôn đi qua có tọa độ là:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1=1\end{matrix}\right.\)

\(a,\Leftrightarrow3m-1=-2\Leftrightarrow m=-\dfrac{1}{3}\Leftrightarrow\left(d\right):y=-\dfrac{1}{3}x-1\\ c,\text{Hs góc: }-\dfrac{1}{3}\\ \text{Gọi góc cần tìm là }\alpha>90^0\\ \Leftrightarrow\tan\left(180^0-\alpha\right)=\dfrac{1}{3}\approx\tan18^0\\ \Leftrightarrow\alpha\approx180^0-18^0=162^0\)