Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
![]()
Đạo hàm
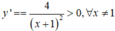
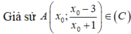
Đường thẳng ∆ là tiếp tuyến của đồ thị (C) tại ∆ nên có hệ số góc là
Phương trình ∆
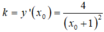
![]()
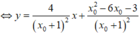
Đồ thị (C) có đường tiệm cận đứng là ∆ 1 : x = - 1 và đường tiệm cận ngang là ∆ 2 : y = 1
![]()
![]()
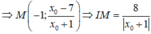
![]()
![]()
Nửa chu vi tam giác IMN là
![]()
Dấu "=" xảy ra khi
![]()
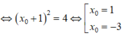
Bán kính đường tròn nội tiếp tam giác IMN là
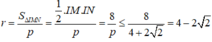

Đáp án B
Tâm đối xứng của đồ thị (C) là giao điểm hai đường tiệm cận. (C) có tiệm cận đứng là x=-1, tiệm cận ngang là y=2 => I(-1;2)
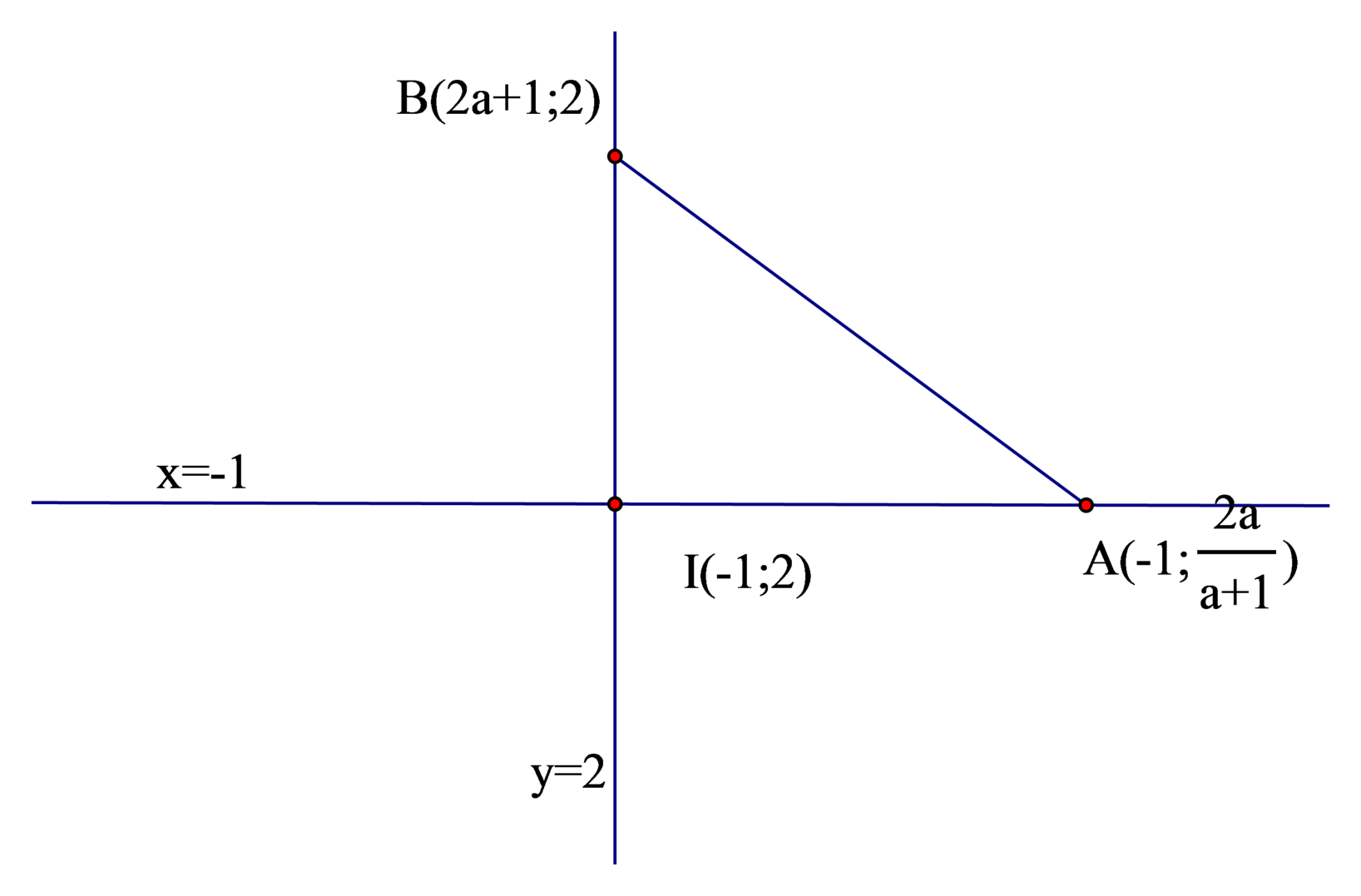
Ta có: y ' = 1 x + 1 2 ⇒ PTTT tại điểm M a ; b là y = 1 a + 1 2 x − a + 2 a + 1 a + 1 . Từ đây ta xác định được giao điểm của PTTT tại M a ; b và hai tiệm cận x = − 1 , y = 2 là A − 1 ; 2 a a + 1 , B 2 a + 1 ; 2 .
Độ dài các cạnh của Δ I A B như sau
I A = 2 a a + 1 − 2 = 2 a + 1 I B = 2 a + 1 + 1 = 2 a + 1 A B = 2 1 a + 1 2 + a + 1 2 ⇒ S I A B = 1 2 I A . I B = 2 ;
P = I A + I B + A B 2 = 1 a + 1 + a + 1 + 1 a + 1 2 + a + 1 2
Áp dụng bất đẳng thức Cosi ta có p ≥ 2 + 2 đạt được ⇔ a + 1 = 1 ⇔ a = 0 ⇒ b = 1 a = − 2 ⇒ b = 3 ⇒ a + b = 1

Đáp án B
Điểm M ∈ C ⇒ M a ; 2 a + 1 a + 1 ⇒ y ' a = 1 a + 1 2
và y a = 2 a + 1 a + 1 .
Suy ra phương trình tiếp tuyến của ( C) tại M là
y = 2 a + 1 a + 1 = 1 a + 1 2 x − a ⇔ y = x a + 1 2 + 2 a 2 + 2 a + 1 a + 1 2 d .
Đường thẳng ( d ) cắt tiệm cận đứng tại
A − 1 ; 2 a a + 1 ⇒ I A = 2 a + 1 .
Đường thẳng ( d ) cắt tiệm cận ngang tại
B 2 a + 1 ; 2 ⇒ I B = 2 a + 1 .
Suy ra I A . I B = 4 và tam giác IAB vuông tại I
⇒ S Δ I A B = 1 2 . I A . I B = 2
Mà S Δ I A B = I A + I B + I C 2 x r ⇒ r m ax
khi và chỉ khi I A + I B + I C min
Ta có
I A + I B + I C = I A + I B + I A 2 + I B 2 ≥ 2 I A . I B + 2 I A . I B = 4 + 4 2 .
Dấu “=” xảy ra
⇔ 2 a + 1 = 2 a + 1 ⇔ a + 1 2 = 1 ⇔ a = 0 ⇒ b = 1 a = − 2 ⇒ b = 3 ⇒ a + b = 1.

Đáp án C.
Ta có I 2 ; 1 .
Tiếp tuyến với C tại điểm M x 0 ; x 0 + 2 x 0 − 2 là d : y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2
Tọa độ A là nghiệm của hệ
y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2 x = 2 ⇒ y = 4 x 0 − 2 + x 0 + 2 x 0 − 2 ⇒ A 2 ; x 0 + 6 x 0 − 2 ⇒ I A → = 0 ; 8 x 0 − 2
Tọa độ B là nghiệm của hệ
y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2 y = 2 ⇒ x 0 − 2 2 = − 4 x − x 0 + x 0 2 − 4 ⇒ B 2 x 0 − 2 ; 1 ⇒ I B → = 2 x 0 − 4 ; 0 Do đó C I A B = π . A B = π I A 2 + I B 2 ≥ π 2 I A . I B
Mà I A . I B = 8 x 0 − 2 . 2 x 0 − 4 = 16 ⇒ C I A B ≥ 4 π 2

vì đồ thị hàm số đi qua điểm \(A\left(-1;\frac{5}{2}\right)\) nên tọa độ của A thỏa mãn phương trình sau: \(\frac{a+b}{-2}=\frac{5}{2}\Rightarrow a+b=-5\)(*)
ta tính y' có:
\(y'=\frac{\left(2ax-b\right)\left(x-1\right)-\left(ax^2-bx\right)}{\left(x-1\right)^2}=\frac{2ax^2-2ax-bx+b-ax^2+bx}{\left(x-1\right)^2}=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\)
vì hệ số góc của tiếp tuyến tại điểm O(0;0) bằng 3 nên \(y'\left(O\right)=\frac{b}{\left(0-1\right)^2}=-3\Rightarrow b=-3\)
thay b=-3 vào (*) ta tìm được a=-2
vậy a=-2;b=-3

Phương trình tiếp tuyến tại M0 có dạng: y = k(x – x0) + y0 (*)
Với x0 là hoành độ tiếp điểm;
Với y0 = f(x0) là tung độ tiếp điểm;
Với k = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.
Để viết được phương trình tiếp tuyến ta phải xác định được x0; y0 và k

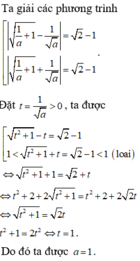


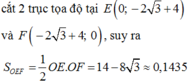



Chọn đáp án A
Chú ý: Ta có một số bài toán có thể giải bằng công thức tính nhanh
tại M tạo với hai tiệm cận
a. Một tam giác vuông cân.
b. Một tam giác vuông có cạnh huyền nhỏ nhất.
c. Một tam giác có chu vi nhỏ nhất.
d. Một tam giác có bán kính đường tròn ngoại tiếp nhỏ nhất.
e. Một tam giác có bán kính đường tròn nội tiếp lớn nhất.
5. Tìm 2 điểm thuộc hai nhánh khác nhau của đồ thị (C) sao cho tiếp tuyến tại và song song với nhau đồng thời MN đạt giá trị nhỏ nhất.
Công thức tính nhanh cho các bài toán trên như sau:
Hoành độ điểm M(hoặc hoành độ hai điểm M và N) cần tìm là nghiệm của phương trình y ' 2 = 1