Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hàm số đồng biến
(=) m-2 >o (=) m>2
Khi m=5
ta có y=(5-2)x+3
=> y=3x+3
Cho x=0 =)y=3 A(0;3)
Cho y=0 =) x=-1 B(-1;0)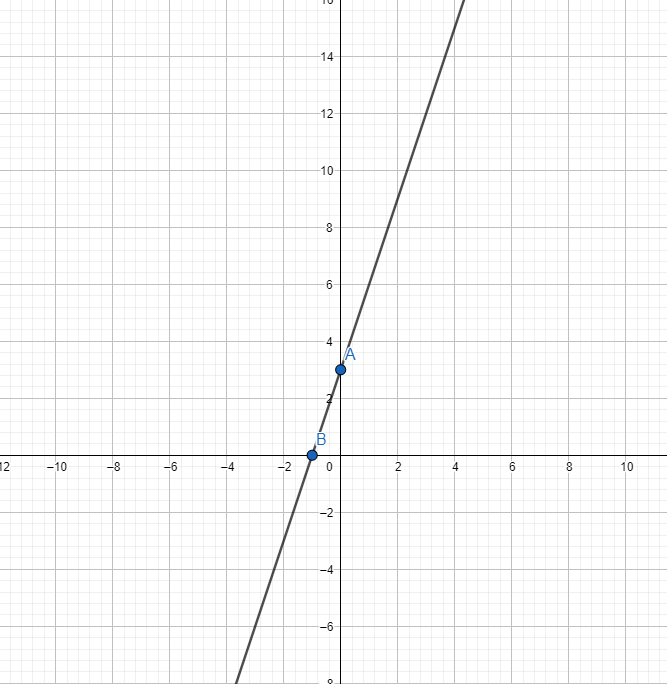
y=(m-2)x+3 (m≠2)
a) Để y=(m-2)x+3 đồng biến.
m-2>0⇔m>2
Vậy m>2 để hàm số đồng biến
b) Thay m=5 vào hàm số ➜ y=3x+3
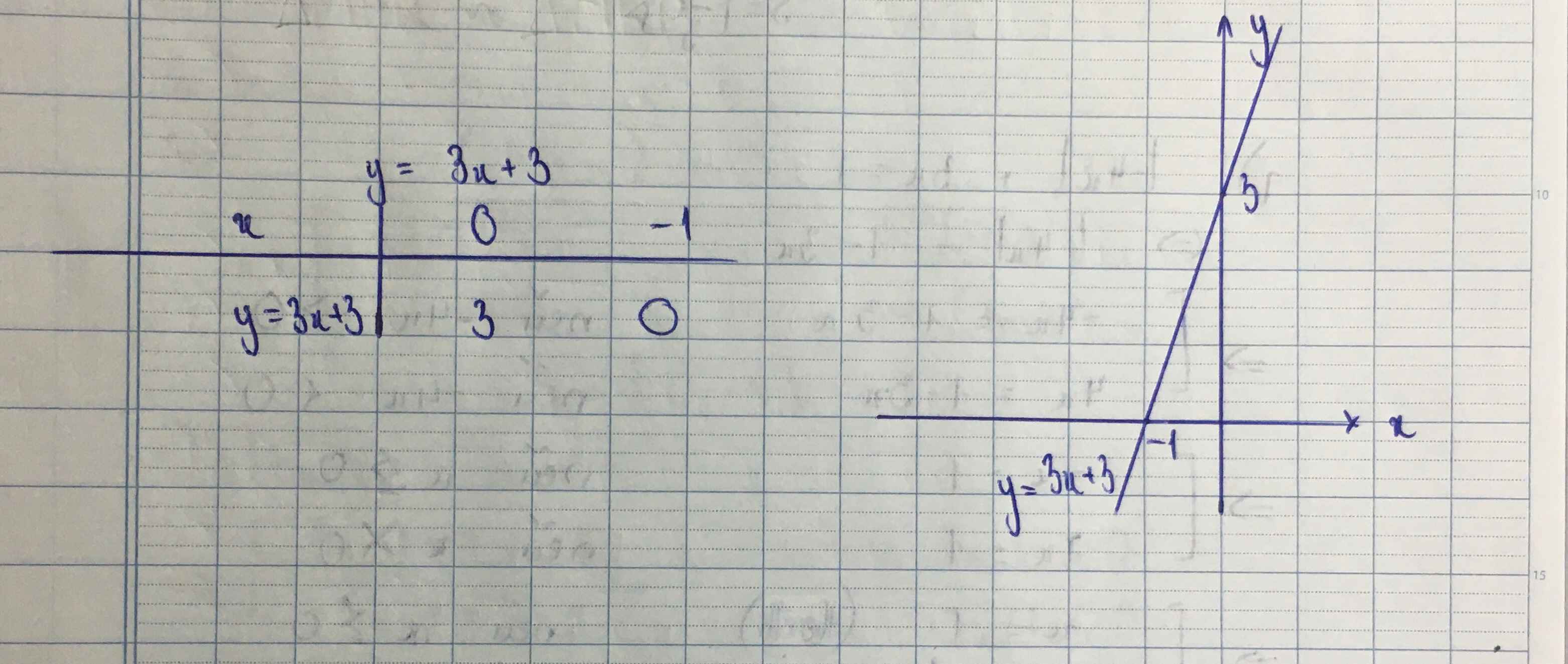

a: Để hàm số đồng biến trên R thì m-2>0
hay m>2
b: Thay x=0 và y=5 vào hàm số, ta được:
m+3=5
hay m=2

a: Để hàm số đồng biến thì m-2>0
hay m>2
b: Thay x=0 và y=5 vào hàm số,ta được:
\(m+3=5\)
hay m=2

a: Để hàm số đồng biến thì m-2>0
hay m>2
b: Thay x=0 và y=5 vào hàm số,ta được:
\(m+3=5\)
hay m=2

Câu 1:
a) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(3m+5< 0\)
\(\Leftrightarrow3m< -5\)
hay \(m< -\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(m< -\dfrac{5}{3}\)
b) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì
3m+5>0
\(\Leftrightarrow3m>-5\)
hay \(m>-\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì \(m>-\dfrac{5}{3}\)
2.
Để hàm nghịch biến với x>0 \(\Leftrightarrow\sqrt{3k+4}-3< 0\)
\(\Leftrightarrow\sqrt{3k+4}< 3\Leftrightarrow3k+4< 9\)
\(\Rightarrow-\dfrac{4}{3}\le k< \dfrac{5}{3}\)
Để hàm đồng biến khi x>0
\(\Leftrightarrow\sqrt{3k+4}-3>0\Leftrightarrow\sqrt{3k+4}>3\)
\(\Leftrightarrow3k+4>9\Rightarrow k>\dfrac{5}{3}\)

\(a,HSĐB\Leftrightarrow-\dfrac{3}{2}m+5>0\Leftrightarrow m>\dfrac{10}{3}\\ b,m=2\Rightarrow y=2x-6\\ Chọn.3.điểm:A\left(0;-6\right);B\left(2;-2\right);C\left(3;0\right)\)
Anh chọn điểm em tự vẽ đồ thị hi
a) Hàm số đồng biến khi:
-3m/2 + 5 > 0
⇔ -3m/2 > -5
⇔ m < 10/3
b) m = 2
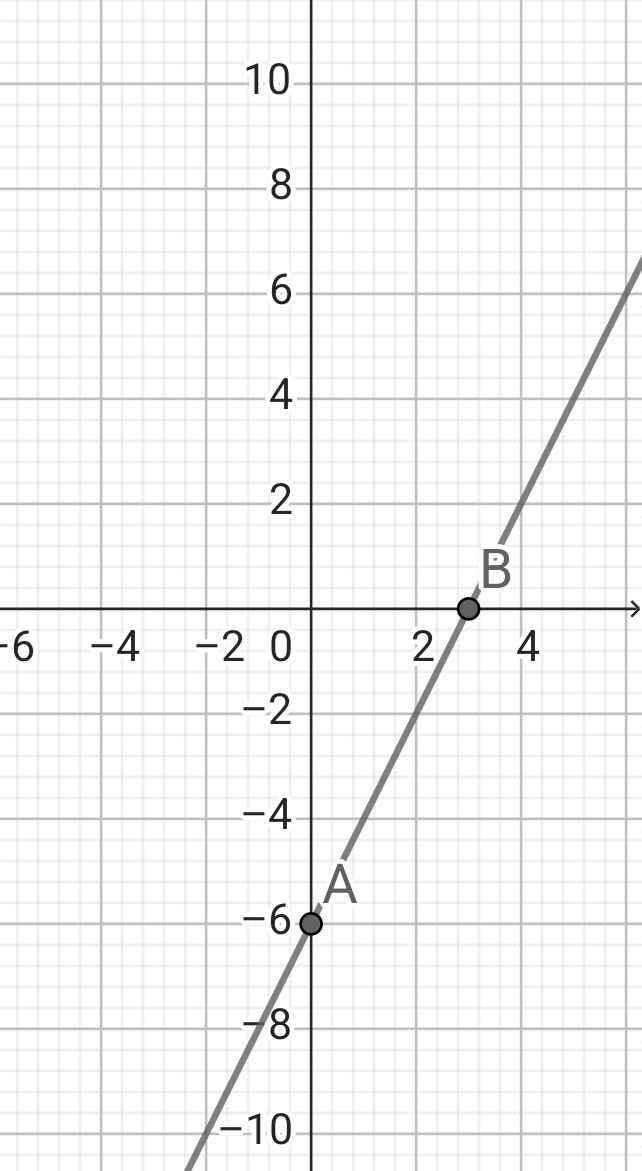
⇔ y = 2x - 6
Cho x = 0 thì y = -6 ⇒ A(0; -6)
y = 0 thì x = 3 ⇒ B(3; 0)
*) Đồ thị:


a) Để (d) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào (d), ta được:
\(m-1+5=2\)
\(\Leftrightarrow m+4=2\)
hay m=-2
Vậy: m=-2

Bài 1:
Để hàm số y=(2-m)x-2 là hàm số bậc nhất thì 2-m<>0
=>m<>2
a=2-m
b=-2
Bài 2:
a: Để hàm số y=(m-5)x+1 đồng biến trên R thì m-5>0
=>m>5
b: Để hàm số y=(m-5)x+1 nghịch biến trên R thì m-5<0
=>m<5
Bài 3:
a: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}3-m=2\\2\ne m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=1\)
b: Để (d1) cắt (d2) thì \(3-m\ne2\)
=>\(m\ne1\)
c: Để (d1) cắt (d2) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}3-m\ne2\\m=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m=2\end{matrix}\right.\)
=>m=2
Để hàm số đồng biến với mọi x < 0 thì a < 0
nên 2 5 − 2 m < 0
⇔ 5 – 2m < 0 (do 2 > 0) ⇔ 2m > 5 ⇔ m > 5 2
Vậy m > 5 2 thỏa mãn điều kiện đề bài
Đáp án cần chọn là: A