Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đang học Lý mà thấy bài nguyên hàm hay hay nên nhảy vô luôn :b
\(I_1=\int\limits^1_0xf\left(x\right)dx\)
\(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=xdx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\dfrac{1}{2}x^2\end{matrix}\right.\)
\(\Rightarrow\int xf\left(x\right)dx=\dfrac{1}{2}x^2f\left(x\right)-\dfrac{1}{2}\int x^2f'\left(x\right)dx\)
\(\Rightarrow\int\limits^1_0xf\left(x\right)dx=\dfrac{1}{2}x^2|^1_0-\dfrac{1}{2}\int\limits^1_0x^2f'\left(x\right)dx=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{1}{2}\int\limits^1_0\left[f'\left(x\right)\right]^2dx=\dfrac{3}{10}\Rightarrow\int\limits^1_0x^2f'\left(x\right)dx=\dfrac{3}{5}\)
Đoạn này hơi rối xíu, ông để ý kỹ nhé, nhận thấy ta có 2 dữ kiện đã biết, là: \(\int\limits^1_0\left[f'\left(x\right)\right]^2dx=\dfrac{9}{5}and\int\limits^1_0x^2f'\left(x\right)dx=\dfrac{3}{5}\) có gì đó liên quan đến hằng đẳng thức, nên ta sẽ sử dụng luôn
\(\int\limits^1_0\left[f'\left(x\right)+tx^2\right]^2dx=0\)
\(\Leftrightarrow\int\limits^1_0\left[f'\left(x\right)\right]^2dx+2t\int\limits^1_0x^2f'\left(x\right)dx+t^2\int\limits^1_0x^4dx=0\)
\(\Leftrightarrow\dfrac{9}{5}+\dfrac{6}{5}t+\dfrac{1}{5}t^2=0\) \(\left(\int\limits^1_0x^4dx=\dfrac{1}{5}x^5|^1_0=\dfrac{1}{5}\right)\)\(\)\(\Leftrightarrow t=-3\Rightarrow\int\limits^1_0\left[f'\left(x\right)-3x^2\right]^2dx=0\)
\(\Leftrightarrow f'\left(x\right)=3x^2\Leftrightarrow f\left(x\right)=x^3+C\)
\(\Rightarrow\int\limits^1_0f\left(x\right)dx=\int\limits^1_0x^3dx=\dfrac{1}{4}x^4|^1_0=\dfrac{1}{4}\)
P/s: Có gì ko hiểu hỏi mình nhé !

\(3\int\limits^1_0\left[f'\left(x\right).f^2\left(x\right)+\frac{1}{9}\right]dx\le2\int\limits^1_0\sqrt{f'\left(x\right)}f\left(x\right)dx\) (1)
Ta lại có:
\(3f'\left(x\right).f^2\left(x\right)+\frac{1}{3}\ge2\sqrt{f'\left(x\right)}.f\left(x\right)\)
\(\Rightarrow3\int\limits^1_0\left[f'\left(x\right).f^2\left(x\right)+\frac{1}{9}\right]\ge2\int\limits^1_0\sqrt{f'\left(x\right)}.f\left(x\right)dx\) (2)
Từ (1); (2) \(\Rightarrow3\int\limits^1_0\left[f'\left(x\right).f^2\left(x\right)+\frac{1}{9}\right]dx=2\int\limits^1_0\sqrt{f'\left(x\right)}.f\left(x\right)dx\)
Dấu "=" xảy ra khi và chỉ khi:
\(3f'\left(x\right).f^2\left(x\right)=\frac{1}{3}\Rightarrow3\int f'\left(x\right).f^2\left(x\right)dx=\int\frac{1}{3}dx\)
\(\Rightarrow f^3\left(x\right)=\frac{x}{3}+C\)
Thay \(x=0\Rightarrow f^3\left(0\right)=C\Rightarrow C=1\)
\(\Rightarrow f^3\left(x\right)=\frac{x}{3}+1\Rightarrow\int\limits^1_0f^3\left(x\right)dx=\int\limits^1_0\left(\frac{x}{3}+1\right)dx=\frac{7}{6}\)
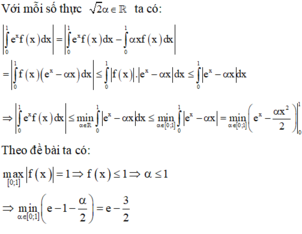
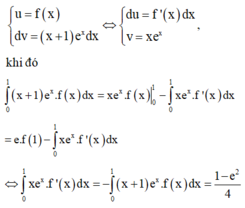
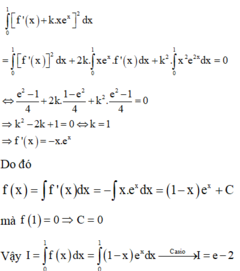
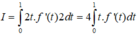
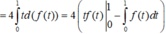
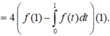
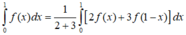
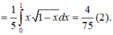
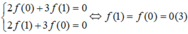
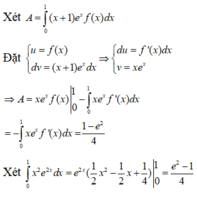
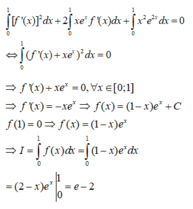
\(f'\left(x\right)=f'\left(1-x\right)\Rightarrow\int f'\left(x\right)dx=\int f'\left(1-x\right)dx\)
\(\Rightarrow f\left(x\right)=-f\left(1-x\right)+C\Rightarrow f\left(x\right)+f\left(1-x\right)=C\)
Thay \(x=0\Rightarrow f\left(0\right)+f\left(1\right)=C\Rightarrow C=42\)
\(\Rightarrow\int\limits^1_0\left[f\left(x\right)+f\left(1-x\right)\right]dx=\int\limits^1_042dx=42\)
Xét \(I=\int\limits^1_0f\left(1-x\right)dx\)
Đặt \(1-x=u\Rightarrow dx=-du;\left\{{}\begin{matrix}x=0\Rightarrow u=1\\x=1\Rightarrow u=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_1f\left(u\right).\left(-du\right)=\int\limits^1_0f\left(u\right).du=\int\limits^1_0f\left(x\right)dx\)
\(\Rightarrow2\int\limits^1_0f\left(x\right)dx=42\Rightarrow\int\limits^1_0f\left(x\right)dx=21\)