
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

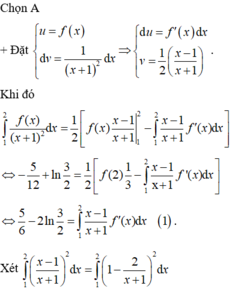
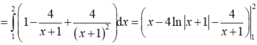
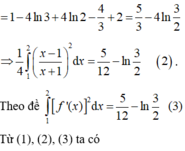
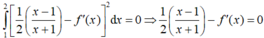
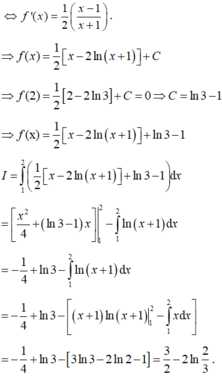

Chọn D.
Xét I = ∫ 0 1 f ' x d x Đặt t = x → t 2 = x → 2 t d t = d x
Đổi cận x = 0 → t = 0 x = 1 → t = 1 . Khi đó I = 2 ∫ 0 1 t f ' ( t ) d t = 2 A
Tính A = ∫ 0 1 t f ' ( t ) d t . Đặt u = t d v = f ' t d t → d u = d t v = f t
Khi đó
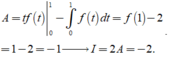

Theo bất đẳng thức Cauchy-Schwarz cho tích phân có:
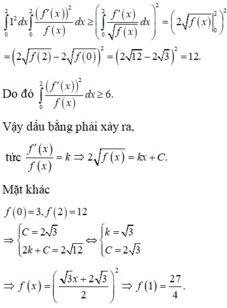
Đáp án A

\(f\left(x\right)-\left(x+1\right)f'\left(x\right)=2x.f^2\left(x\right)\)
\(\Rightarrow\dfrac{f\left(x\right)-\left(x+1\right)f'\left(x\right)}{f^2\left(x\right)}=2x\)
\(\Rightarrow\left[\dfrac{x+1}{f\left(x\right)}\right]'=2x\)
Lấy nguyên hàm 2 vế:
\(\dfrac{x+1}{f\left(x\right)}=\int2xdx=x^2+C\)
Thay \(x=1\Rightarrow\dfrac{2}{f\left(1\right)}=1+C\Rightarrow C=0\)
\(\Rightarrow f\left(x\right)=\dfrac{x+1}{x^2}\Rightarrow\int\limits^2_1\left(\dfrac{1}{x}+\dfrac{1}{x^2}\right)dx=\left(lnx-\dfrac{1}{x}\right)|^2_1=ln2+\dfrac{1}{2}\)

2a. Đề sai, nhìn biểu thức \(\dfrac{f'\left(x\right)}{f'\left(x\right)}dx\) là thấy
2b. Đồ thị hàm số không cắt Ox trên \(\left(0;1\right)\) nên diện tích cần tìm:
\(S=\int\limits^1_0\left(x^4-5x^2+4\right)dx=\dfrac{38}{15}\)
3a. Phương trình (P) theo đoạn chắn:
\(\dfrac{x}{4}+\dfrac{y}{-1}+\dfrac{z}{-2}=1\)
3b. Câu này đề sai, đề cho mặt phẳng (Q) rồi thì sao lại còn viết pt mặt phẳng (Q) nữa?
sorry thầy em xin sửa lại câu 3 b là
b) trong không gian Oxyz cho mặt phẳng (Q): 3x-y-2z+1=0.Viết phương trình mặt phẳng (P) song song với mặt phẳng (Q) và đi qua điểm M(0;0;1)