K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2020
Do \(x< 2\) nên x chỉ tiến tới 2 từ phía trái
Do đó hàm số chỉ có giới hạn trái tại điểm x=2 (giới hạn bằng dương vô cực)

CM
30 tháng 10 2019
+ A đúng theo định nghĩa.
+ B đúng. Vì:
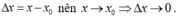
+ C đúng.
- Đặt:
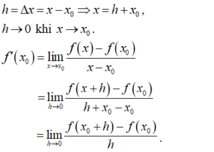
+ Vậy D sai.
Chọn D
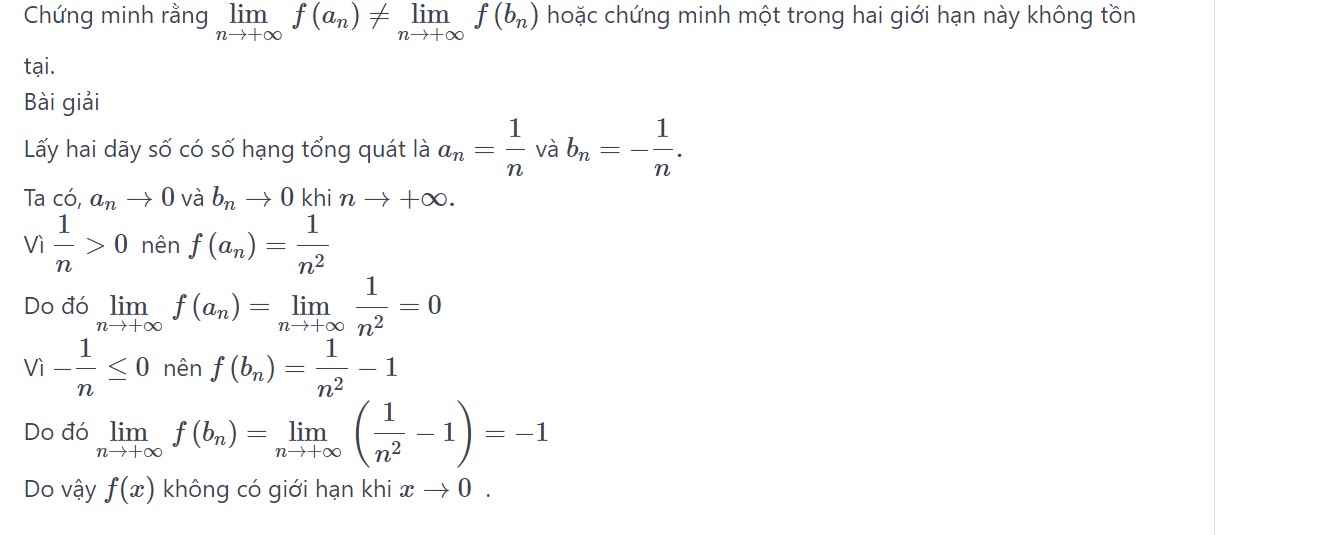
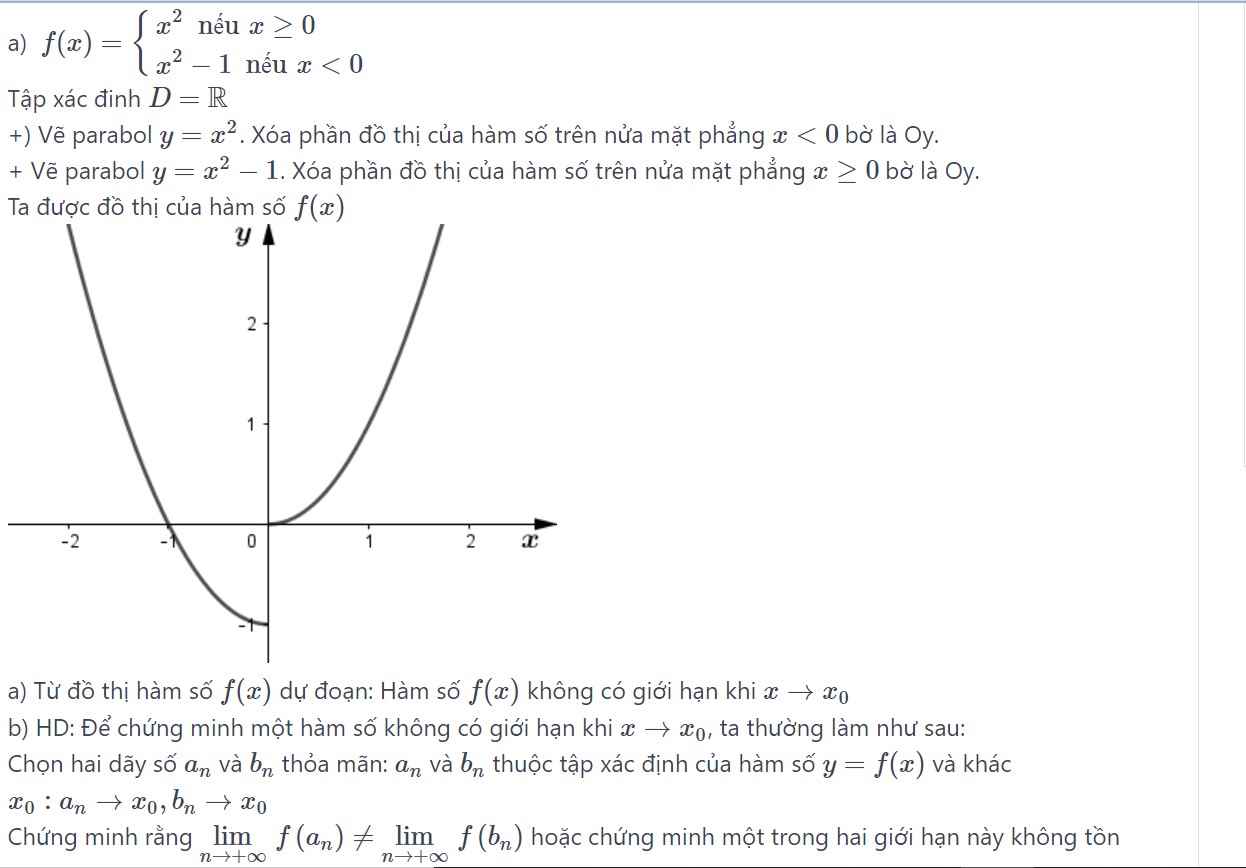

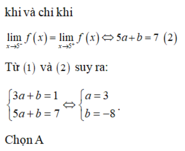
Đáp án D sai
Hàm đa thức có giới hạn tại mọi điểm và tại tất cả các điểm thì giới hạn trái luôn bằng giới hạn phải