Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt t = f ( f ( x ) - 1 ) - 2 phương trình trở thành:
f ( t ) = 1 ⇔ t 4 - 4 t 2 + 1 = 1 ⇔ t = 0 ; t = ± 2
TH1: Nếu
t = 0 ⇔ f ( f ( x ) - 1 ) - 2 = 0 ⇔ f ( f ( x ) - 1 ) = 2
Đặt a=f(x)-1 phương trình trở thành:
f ( a ) = 2 ⇔ a 4 - 4 a 2 - 1 = 0 ⇔ a = ± 2 + 5
Nhận xét: Xét hàm số y = f ( x ) - 1 = x 4 - 4 x 2 có y c d = y ( 0 ) = 0 ; y c t = y ± 2 = - 4
Với a ∈ - 4 ; 0 phương trình y = a có bốn nghiệm thực phân biệt. Với a = 0 phương trình y = a có hai nghiệm thực phân biệt. Với a < -4 phương trình y = a vô nghiệm.
Áp dụng cho trường này có 2 + 4 = 6 nghiệm.
TH2: Nếu
t = - 2 ⇔ f ( f ( x ) - 1 ) - 2 = - 2 ⇔ f ( f ( x ) - 1 ) = 0
Đặt a=f(x)-1 phương trình trở thành:
f ( a ) = 0 ⇔ a 4 - 4 a 2 + 1 = 0 ⇔ a = ± 2 + 3
Trường hợp này có 2 + 2 + 4 + 4 = 12 nghiệm.
TH3: Nếu t = 2 ↔ f ( f ( x ) - 1 ) = 4 Đặt a=f(x)-1 phương trình trở thành:
f ( a ) = 4 ⇔ a 4 - a = ± 4 a 2 - 3 = 0 ⇔ a = ± 2 + 7
Trường hợp này có 2 + 4 = 6 nghiệm.
Vậy phương trình đã cho có tất cả 24 nghiệm thực phân biệt.
Chọn đáp án A.

Ta có ![]()
Do đó hàm số f(x) đồng biến trên R. Với một hàm số f(x) đồng biến trên R ta có tính chất sau:
![]() Thật vậy
Thật vậy
+) Nếu ![]()
![]() (vô lí);
(vô lí);
+) Nếu ![]()
![]() (vô lí).
(vô lí).
+) Nếu ![]()
![]() (thỏa mãn)/
(thỏa mãn)/
Từ ba khả năng trên ta có điều phải chứng minh. Áp dụng tính chất này ta có:
![]()
![]()
![]()
Phương trình đã cho có ba nghiệm thực phân biệt khi và chỉ khi (*) có ba nghiệm thực phân biệt
![]()
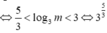
![]()
Có tất cả 20 số nguyên thỏa mãn.
Chọn đáp án A.

Đáp án D
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]

Đáp án D
Định lí: “Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho f c = 0 ”.
Mệnh đề 1: SAI ở giả thiết (a;b).
Mệnh đề 2: Nếu hàm số y=f(x) liên tục trên a ; b
và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho c hay f x = 0 là nghiệm của phương trình f(x)=0 nên mệnh đề 2 ĐÚNG.
Mệnh đề 3: Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì đồ thị hàm số y=f(x) cắt trục Ox tại duy nhất một điểm thuộc khoảng (a;b) nên f(x)=0 có nghiệm duy nhất trên (a;b). Do đó mệnh đề 3 ĐÚNG

Đáp án là D
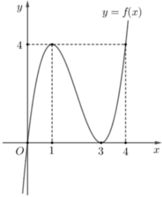
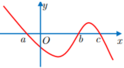
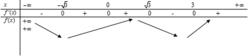
Từ đồ thị f ’(x) ta lập được BBT của f(x)
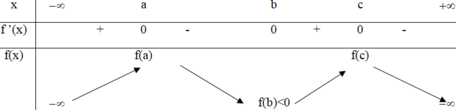
=> Có 4 nghiệm là nhiều nhất

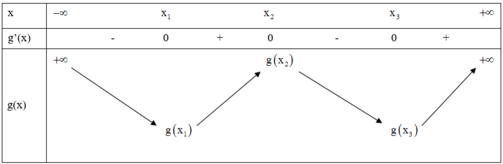
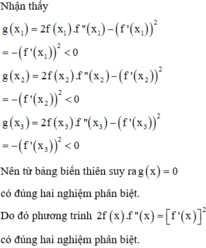


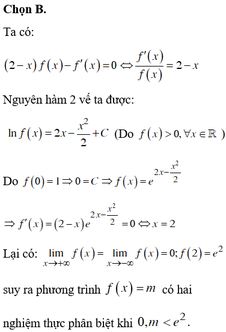
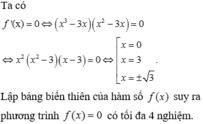
Đáp án C
Cho a = 0 , b = − 3 , c = 0 ⇒ f x = x 3 − 3 x 2 = 0 có 3 nghiệm phân biệt.
Ta có:
f ' x = 3 x 2 − 6 x f ' ' x = 6 x − 6 ⇒ 2 x 3 − 3 x 2 6 x − 6 = 3 x 2 − 6 x 2 ⇔ 12 x 2 x − 3 x − 1 = 9 x 2 x − 2 2 ⇔ x = 0 4 x 2 − 4 x + 3 = 3 x 2 − 4 x + 4 ⇔ x = 0 x = 4