Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
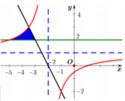
Hoành độ giao điểm của (H) và (d) là nghiệm: x − 1 x + 2 = − 2 x − 4 ⇔ x = − 1 x = − 7 2
Hoành độ giao điểm của (d) và Δ là nghiệm: 2 = − 2 x − 4 ⇔ x = − 3
Hoành độ giao điểm của (H) và Δ là nghiệm: x − 1 x + 2 = 2 ⇔ x = − 5
Khi đó, diện tích hình phẳng cần tính là S = ∫ − 5 − 7 2 x − 1 x + 2 − 2 d x + ∫ − 7 2 − 3 − 2 x − 4 − 2 d x = − 5 4 + 3 ln 2
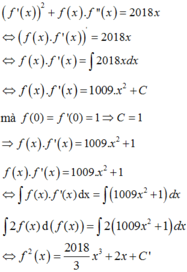
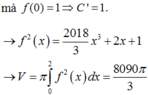
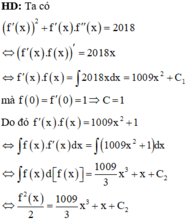

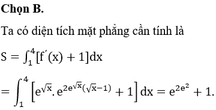
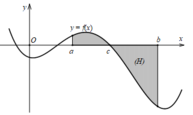
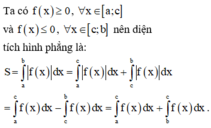

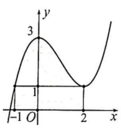
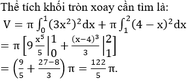
Phương pháp:
Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng