Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Đáp án là D
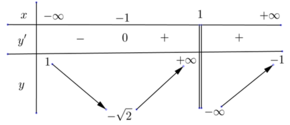
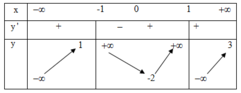
Từ BBT ta có
lim x → + ∞ y = − 1 ; lim x → − ∞ y = 1 do đó đồ thị hàm số có hai đường tiệm cận ngang là
y = 1; y =−1.
lim x → 1 − y = + ∞ ; lim x → 1 − y = − ∞ do đó đồ thị hàm số có một đường tiệm cận đứng là x =1. Vậy tổng số có 3 đường tiệm cận
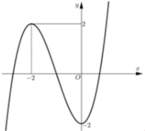
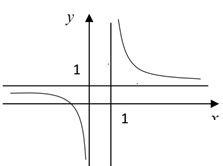
Hình vẽ bên là đồ thị của hàm số y=f(x). Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=f(x) là
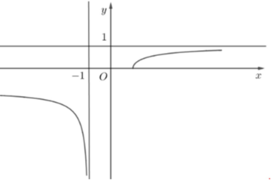

Quan sát đồ thị có ![]()
![]() là tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.
Chọn đáp án A.






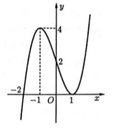
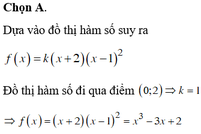
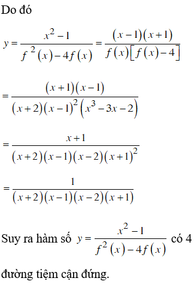

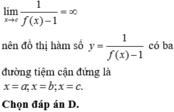
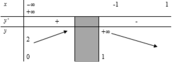

Chọn đáp án C