Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Tọa độ đỉnh của (P) là:
\(\begin{cases}x=-\frac{b}{2a}=\frac{4m}{2\cdot2}=\frac{4m}{4}=m\\ y=-\frac{b^2-4ac}{4a}=-\frac{\left(-4m\right)^2-4\cdot2\cdot5}{4\cdot2}=-\frac{16m^2-40}{8}=-2m^2+5\end{cases}\)
Ta có: \(y=-2m^2+5\le5\forall m\)
Dấu '=' xảy ra khi m=0
b: Phương trình hoành độ giao điểm là:
\(2x^2-4mx+5=5\)
=>\(2x^2-4mx=0\)
=>\(x^2-2mx=0\)
=>x(x-2m)=0
=>\(\left[\begin{array}{l}x=0\\ x=2m\end{array}\right.\)
Để A và B là hai điểm phân biệt thì 2m<>0
=>m<>0
A(0;5); B(2m;5)
\(AB=\sqrt6\)
=>\(AB^2=6\)
=>\(\left(2m-0\right)^2+\left(5-5\right)^2=6\)
=>\(4m^2=6\)
=>\(m^2=\frac64\)
=>\(\left[\begin{array}{l}m=\frac{\sqrt6}{2}\left(nhận\right)\\ m=-\frac{\sqrt6}{2}\left(nhận\right)\end{array}\right.\)
Cho hàm số \(y = 2{x^2} + x + m\). Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5.
Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 1}}{{2.2}} = - \frac{1}{4};{y_S} = f( - \frac{1}{4}) = 2{\left( { - \frac{1}{4}} \right)^2} + \left( { - \frac{1}{4}} \right) + m = m - \frac{1}{8}\)
Ta có: \(a = 2 > 0\), hàm số có bảng biến thiên dạng:
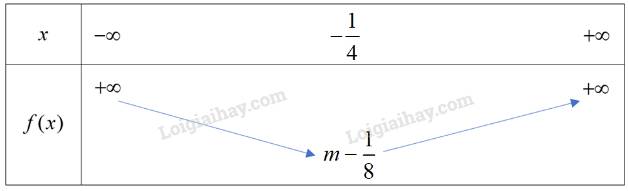
Hàm số đạt giá trị nhỏ nhất bằng \(m - \frac{1}{8} = 5 \Leftrightarrow m = \frac{{41}}{8}.\)
Vậy \(m = \frac{{41}}{8}\) thì hàm số đạt giá trị nhỏ nhất bằng 5.
b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)
ta có hàm số
\(y=2\left(x^2-2mx+m^2\right)-\left(2m^2+m-5\right)\ge-\left(2m^2+m-5\right)\)
vậy \(-\left(2m^2+m-5\right)=5\Leftrightarrow2m^2+m=0\Leftrightarrow\orbr{\begin{cases}m=0\\m=-\frac{1}{2}\end{cases}}\)
Vậy có hai giá trị của m