Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tham khảo:
a) Ta có: \(\overrightarrow b = \left( {4; - 1} \right)\) và \(\overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j \;\; \Rightarrow \;\overrightarrow a \;\left( {3; - 2} \right)\)
\( \Rightarrow 2\;\overrightarrow a - \overrightarrow b = \left( {2.3 - 4\;;\;2.\left( { - 2} \right) - \left( { - 1} \right)} \right) = \left( {2; - 3} \right)\)
Lại có: M (-3; 6), N(3; -3)
\( \Rightarrow \overrightarrow {MN} = \left( {3 - \left( { - 3} \right); - 3 - 6} \right) = \left( {6; - 9} \right)\)
Dễ thấy:\(\left( {6; - 9} \right) = 3.\left( {2; - 3} \right)\) \( \Rightarrow \overrightarrow {MN} = 3\left( {2\;\overrightarrow a - \overrightarrow b } \right)\)
b) Ta có: \(\overrightarrow {OM} = \left( { - 3;6} \right)\) ( do M(-3; 6)) và \(\overrightarrow {ON} = \left( {3; - 3} \right)\) (do N (3; -3)).
Hai vectơ này không cùng phương (vì \(\frac{{ - 3}}{3} \ne \frac{6}{{ - 3}}\)).
Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
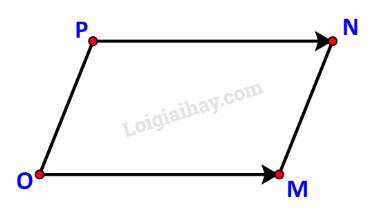
c) Các điểm O, M, N không thẳng hàng nên OMNP là một hình hành khi và chỉ khi \(\overrightarrow {OM} = \overrightarrow {PN} \).
Do \(\overrightarrow {OM} = \left( { - 3;6} \right),\;\overrightarrow {PN} = \left( {3 - x; - 3 - y} \right)\) nên
\(\overrightarrow {OM} = \overrightarrow {PN} \Leftrightarrow \left\{ \begin{array}{l} - 3 = 3 - x\\6 = - 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 9\end{array} \right.\)
Vậy điểm cần tìm là P (6; -9).
a) Tọa độ của vectơ \(\overrightarrow a \) là \(\left( {2;7} \right)\)
b) Tọa độ của vectơ \(\overrightarrow b \) là \(\left( { - 1;3} \right)\)
c) Tọa độ của vectơ \(\overrightarrow c \) là \(\left( {4;0} \right)\)
d) Tọa độ của vectơ \(\overrightarrow d \) là \(\left( {0; - 9} \right)\)
\(\left|\overrightarrow{a}-2\cdot\overrightarrow{b}\right|=\sqrt{15}\)
=>\(\left(\overrightarrow{a}-2\cdot\overrightarrow{b}\right)\left(\overrightarrow{a}-2\cdot\overrightarrow{b}\right)=15\)
=>\(\overrightarrow{a}\cdot\overrightarrow{a}-4\cdot\overrightarrow{a}\cdot\overrightarrow{b}+4\cdot\overrightarrow{b}\cdot\overrightarrow{b}=15\)
=>\(\left(\left|\overrightarrow{a}\right|\right)^2-4\cdot\overrightarrow{a}\cdot\overrightarrow{b}+4\cdot\left(\overrightarrow{b}\right)^2=15\)
=>\(1^2+4\cdot2^2-4\cdot\overrightarrow{a}\cdot\overrightarrow{b}=15\)
=>\(4\cdot\overrightarrow{a}\cdot\overrightarrow{b}=1+16-15=2\)
=>\(\overrightarrow{a}\cdot\overrightarrow{b}=\frac12\)
b: \(\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(2k\cdot\overrightarrow{a}-\overrightarrow{b}\right)\)
\(=2k\cdot\overrightarrow{a}\cdot\overrightarrow{a}-\overrightarrow{a}\cdot\overrightarrow{b}+2k\cdot\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=2k\cdot\left(\left|\overrightarrow{a}\right|\right)^2+\overrightarrow{a}\cdot\overrightarrow{b}\left(2k-1\right)-\left(\overrightarrow{b}\right)^2\)
\(=2k\cdot1^2+\left(2k-1\right)\cdot\frac12-2^2=2k+k-\frac12-4=3k-\frac92\)
\(\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left(\left|\overrightarrow{a}\right|\right)^2+2\cdot\overrightarrow{a}\cdot\overrightarrow{b}+\left(\left|\overrightarrow{b}\right|\right)^2\)
\(=1^2+2^2+2\cdot\frac12=5+1=6\)
=>\(\left|\overrightarrow{a}+\overrightarrow{b}\right|=\sqrt6\)
\(\left(2k\cdot\overrightarrow{a}-\overrightarrow{b}\right)^2=4k^2\cdot\left(\left|\overrightarrow{a}\right|\right)^2-2\cdot2k\cdot\overrightarrow{a}\cdot\overrightarrow{b}+\left(\overrightarrow{b}\right)^2\)
\(=4k^2\cdot1-4k\cdot\frac12+4=4k^2-2k+4\)
=>\(\left|2k\cdot\overrightarrow{a}-\overrightarrow{b}\right|=\sqrt{4k^2-2k+4}\)
\(cos\left(\left(\overrightarrow{a}+\overrightarrow{b}\right);\left(2k\cdot\overrightarrow{a}-\overrightarrow{b}\right)\right)=cos60^0=\frac12\)
=>\(\frac{3k-4,5}{\sqrt{6\left(4k^2-2k+4\right)}}=\frac12\)
=>\(\sqrt{\frac{\left(3k-4,5\right)^2}{6\left(4k^2-2k+4\right)}}=\frac12\)
=>\(\frac{\left(3k-4,5\right)^2}{6\left(4k^2-2k+4\right)}=\frac14\)
=>\(6\left(4k^2-2k+4\right)=4\left(3k-4,5\right)^2\)
=>\(4\left(9k^2-27k+20,25\right)=6\left(4k^2-2k+4\right)\)
=>\(36k^2-108k+81=24k^2-12k+24\)
=>\(12k^2-96k+57=0\)
=>\(4k^2-32k+19=0\)
=>\(k=\frac{8\pm3\sqrt5}{2}\)
???????????????????????????????????????????????????????????????
b) Ta có :
\(IB=2IC\Leftrightarrow IB=2\left(IB+BC\right)\Leftrightarrow-IB=2BC\Leftrightarrow BI=2BC\)
\(JC=-\frac{1}{2}JA\Leftrightarrow JB+BC=-\frac{1}{2}\left(JB+BA\right)\)
\(\Leftrightarrow\frac{3}{2}JB=-\frac{1}{2}BA-BC\Leftrightarrow JB=-\frac{1}{3}BA-\frac{2}{3}BC\)
\(\Rightarrow BJ=\frac{1}{3}BA+\frac{2}{3}BC\)
\(\Rightarrow IJ=BJ-BI=\frac{1}{3}BA+\frac{2}{3}BC-2BC=\frac{1}{3}BA-\frac{4}{3}BC\)
\(KA=-KB\Leftrightarrow KB+BA=-KB\Leftrightarrow2KB=-BA\)
\(\Rightarrow2BK=BA\Leftrightarrow BK=\frac{1}{2}BA\)
\(\Rightarrow JK=BK-BJ=\frac{1}{2}BA-\frac{2}{3}BC=\frac{1}{6}BA-\frac{2}{3}BC\)
\(=\frac{1}{2}\left(\frac{1}{3}BA-\frac{4}{3}BC\right)=\frac{1}{2}IJ\)
Vậy \(I,J,K\)thẳng hàng
a) Ta có hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \) vuông góc nên \(\overrightarrow i .\overrightarrow j = 0\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} + 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} - 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \(\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right) = {\left( {\overrightarrow i } \right)^2} - {\left( {\overrightarrow j } \right)^2} = {\left| {\overrightarrow i } \right|^2} - {\left| {\overrightarrow j } \right|^2} = 1 - 1 = 0\)
b) Sử dụng kết quả của câu a) ta có:
\(\overrightarrow a .\overrightarrow b = \left( {2\overrightarrow i + 2\overrightarrow j } \right).\left( {3\overrightarrow i - 3\overrightarrow j } \right) = 2.3.\left( {\overrightarrow i + \overrightarrow j } \right).\left( {\overrightarrow i - \overrightarrow j } \right) = 6.0 = 0\)
\(\overrightarrow a .\overrightarrow b = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \)