Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

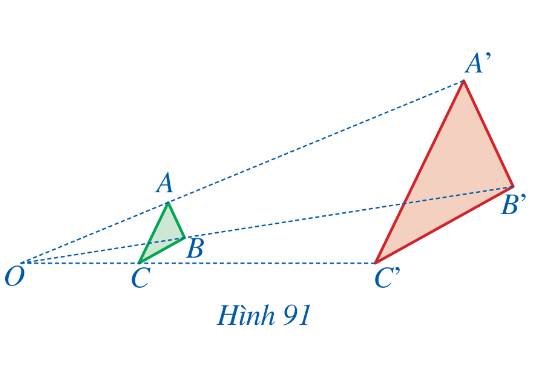
Từ điểm O, ‘‘phóng to’’ ba lần tam giác ABC, ta sẽ nhận được tam giác A’B’C’.

Bạn ghi nhầm đề thì phải, tự nhiên ban đầu có BC+CB, chắc là BC+CD
Sử dụng BĐT tam giác cho các tam giác OAB, OBC, OCD, OAD ta có:
OA+OB>AB; OB+OC>BC; OC+OD>CD; OA+OD>AD
Cộng vế với vế ta được:
2(OA+OB+OC+OD)>AB+BC+CD+AD
\(\Rightarrow OA+OB+OC+OD>\dfrac{AB+BC+CD+AD}{2}\) (1)
Tương tự, sử dụng BĐT tam giác cho các tam giác ABC, BCD, CDA, DAB ta có:
AB+BC>AC=OA+OC
BC+CD>BD=OB+OD
CD+AD>AC=OA+OC
DA+AB>BD=OB+OD
Cộng vế với vế các BĐT trên ta được:
\(2\left(AB+BC+CD+AD\right)>2\left(OA+OB+OC+OD\right)\)
\(\Rightarrow AB+BC+CD+AD>OA+OB+OC+OD\) (2)
Từ (1) và (2) ta có đpcm
Hình bạn vẽ nha bạn.
Áp dụng bất đẳng thức tam giác, ta có:
\(AB< OA+OB\)
\(BC< OB+OC\)
\(CD< OC+OD\)
\(DA< OD+OA\)
Do đó: \(2\left(OA+OB+OC+OD\right)>AB+BC+CD+DA\)
Hay \(OA+OB+OC+OD>\dfrac{AB+BC+CD+DA}{2}\)(1)
Ta lại áp dụng bất đẳng thức tam giác:
\(AB+BC>AC\)
\(BC+CD>BD\)
\(CD+AD>AC\)
\(AB+AD>BD\)
Do đó: \(2\left(AB+BC+CD+DA\right)>2\left(AC+BD\right)\)
Hay \(AB+BC+CD+DA>OA+OB+OC+OD\)(2)
Từ (1) và (2) ta suy ra:
\(\dfrac{AB+BC+CD+DA}{2}< OA+OB+OC+OD< AB+BC+CD+DA\)
Bạn ghi sai cái đề chỗ \(\dfrac{AB+BC+CB+AD}{2}\) nha

Xét hình thang ABCD có EF//AB//CD
nên AE/AD=BF/BC(1)
Xét ΔADC có EO//DC
nên EO/DC=AE/AD(2)
Xét ΔBDC có OF//DC
nên OF/DC=BF/BC(3)
Từ (1), (2) và (3) suy ra OE=OF

A B C A' B' C' O H
a) kẻ đường cao AH.Dễ thấy \(\dfrac{OA'}{AA'}=\dfrac{S_{BOC}}{S_{ABC}}\).Tương tự ta có:
\(\dfrac{OB'}{BB'}=\dfrac{S_{AOC}}{S_{ABC}};\dfrac{OC'}{CC'}=\dfrac{S_{AOB}}{S_{ABC}}\)
\(\Rightarrow\dfrac{OA'}{AA'}+\dfrac{OB'}{BB'}+\dfrac{OC'}{CC'}=\dfrac{S_{BOC}+S_{AOC}+S_{AOB}}{S_{ABC}}=\dfrac{S_{ABC}}{S_{ABC}}=1\left(QED\right)\)
b)Theo câu a:
\(\left(1-\dfrac{OA'}{AA'}\right)+\left(1-\dfrac{OB'}{BB'}\right)+\left(1-\dfrac{OC'}{CC'}\right)=3-1\)
\(\Rightarrow\dfrac{OA}{AA'}+\dfrac{OB}{BB'}+\dfrac{OC}{CC'}=2\)
c)Chứng minh \(\dfrac{OA}{OA'}+\dfrac{OB}{OB'}+\dfrac{OC}{OC'}\ge6\)
\(\Leftrightarrow\dfrac{AA'}{OA'}+\dfrac{BB'}{OB'}+\dfrac{CC'}{OC'}\ge9\)
có:\(\dfrac{AA'}{OA'}=\dfrac{S_{ABC}}{S_{BOC}}\)( theo câu a)
tương tự và cộng lại:\(M=\dfrac{AA'}{OA'}+\dfrac{BB'}{OB'}+\dfrac{CC'}{OC'}=S_{ABC}\left(\dfrac{1}{S_{BOC}}+\dfrac{1}{S_{AOC}}+\dfrac{1}{S_{AOB}}\right)\ge\dfrac{9S_{ABC}}{S_{BOC}+S_{AOB}+S_{AOC}}=\dfrac{9S_{ABC}}{S_{ABC}}=9\)
( BĐT AM-GM)
Dấu = xảy ra hay M nhỏ nhất khi O là trọng tâm của tam giác ABC
d) có: \(\dfrac{AA'}{OA'}=\dfrac{S_{ABC}}{S_{BOC}}\Rightarrow\dfrac{AA'-OA'}{OA'}=\dfrac{S_{ABC}-S_{BOC}}{S_{BOC}}\)
\(\Rightarrow\dfrac{OA}{OA'}=\dfrac{S_{AOC}+S_{AOB}}{S_{BOC}}\)
Tương tự và nhân lại:
\(N=\dfrac{OA}{OA'}.\dfrac{OB}{OB'}.\dfrac{OC}{OC'}=\dfrac{\left(S_{AOC}+S_{AOB}\right)\left(S_{BOC}+S_{AOB}\right)\left(S_{BOC}+S_{AOC}\right)}{S_{AOB}.S_{AOC}.S_{BOC}}\)
Đặt \(\left(S_{BOC};S_{AOB};S_{AOC}\right)\rightarrow\left(a,b,c\right)\)
Thì \(N=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}\)
Theo AM-GM:\(N\ge\dfrac{2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ac}}{abc}=\dfrac{8abc}{abc}=8\)
Dấu = xảy ra khi O là trọng tâm của tam giác ABC

a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó; ΔOAB\(\sim\)ΔOCD
Suy ra: OA/OC=OB/OD
hay \(OA\cdot OD=OB\cdot OC\)
b: Ta có; ΔOAB\(\sim\)ΔOCD
nên AB/CD=OB/OD=OA/OC
=>5/CD=OB/3,6=2/4=1/2
=>CD=10cm; OB=1,8(cm)

Gọi BH là đường cao của ∆ABO
Ta có 2SAOB = OA . BH
Nhưng BH ≤ BO nên 2SAOB ≤ OA . OB
mà OA.OB
Do đó 2SAOB
Dấu “=” xảy ra OA OB và OA = OB
Chứng minh tương tự ta có:
2SBOC ; 2SCOD
2SAOD
Vậy 2S = 2(SAOB + SBOC + SCOD + SDOA) ≤
Hay 2S ≤ OA2 + OB2 + OC2 + OD2
Dấu bằng xẩy ra khi và chỉ khi OA = OB = OC = OD
và là hình vuông tâm O.

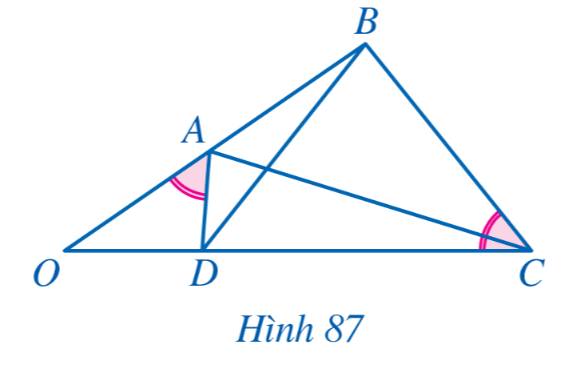
a) Xét tam giác OAD và tam giác OCB có:
\(\widehat {OAD} = \widehat {OCB};\,\,\widehat O\) chung
\( \Rightarrow \Delta OAD \backsim \Delta OCB\) (g-g)
b) Vì \(\Delta OAD \backsim \Delta OCB\) nên ta có \(\frac{{OA}}{{OC}} = \frac{{OD}}{{OB}}\) (Tỉ số đồng dạng)
\( \Rightarrow \frac{{OA}}{{OD}} = \frac{{OC}}{{OB}}\)
c) Xét tam giác OAC và tam giác ODB có:
\(\frac{{OA}}{{OD}} = \frac{{OC}}{{OB}}\) và \(\widehat O\) chung
\( \Rightarrow \Delta OAC \backsim \Delta ODB\) (c-g-c)
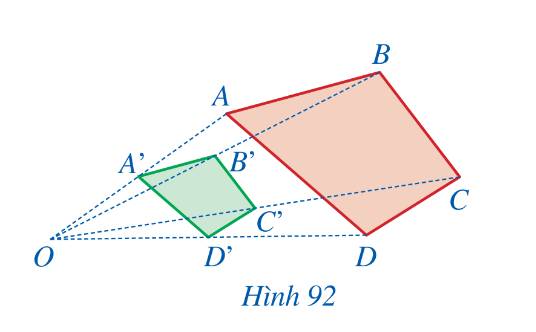
Từ điểm O, ‘‘thu nhỏ’’ hai lần tứ giác ABCD, ta sẽ nhận được tứ giác A’B’C’D’.