Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)
=>\(\left\{{}\begin{matrix}m-1>2\\m+3\le5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>3\\m\le2\end{matrix}\right.\)(vô lý)
vậy ko tồn tại m

Để A và B có nghĩa \(\Rightarrow\left\{{}\begin{matrix}m-1< 4\\2m+2>-2\end{matrix}\right.\) \(\Rightarrow-2< m< 5\)
a/ \(m-1< 2m+2\Rightarrow m>-3\)
Kết hợp điều kiện \(\Rightarrow-2< m< 5\)
b/ \(\left\{{}\begin{matrix}m-1\le-2\\4< 2m+2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\le-1\\m>1\end{matrix}\right.\) \(\Rightarrow-1\le m< 1\)

Để A là tập con của B thì m-1>=-2 và 4<=2m+2 và m-1<=4 và 2m+2>=-2
=>m>=-1 và 2m+2>=4 và m<=3 và m>=-2
=>m>=-1 và m>=1 và -2<=m<=3
=>m>=1 và -2<=m<=3
=>-2<=m<=1

1. \(A\cap B\ne\varnothing\\ \Rightarrow\left\{{}\begin{matrix}m+2\ge2m\\m\le2m+3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m\le2\\m\ge-3\end{matrix}\right.\Rightarrow-3\le m\le2\)
2. A là đoạn có độ dài bằng 5 thì:
\(\left|8-m-m\right|=5\\ \Leftrightarrow\left|8-2m=5\right|\\ \Rightarrow\left\{{}\begin{matrix}8-2m=5\\2m-8=5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=\frac{3}{2}\\m=\frac{11}{2}\end{matrix}\right.\)
3.\(A\cap B=A\Rightarrow\left\{{}\begin{matrix}m\ge-1\\m+5\le3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m\ge-1\\m\le-2\end{matrix}\right.\)

\(A=\left[m;m+1\right]\)
\(B=\left[0;3\right]\)
\(A\cap B=\varnothing\)
\(\Leftrightarrow\left[{}\begin{matrix}m+1< 0\\m>3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>3\end{matrix}\right.\) thỏa mãn đề bài

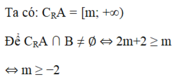
\(P=\left(-\infty;2m-3\right);Q=\left(m-1;+\infty\right)\)
Để \(P\cap Q=\varnothing\Leftrightarrow m-1>2m-3\Leftrightarrow m< 2\)
\(\Rightarrow m\in\left(-\infty;2\right)\)