Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
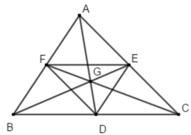
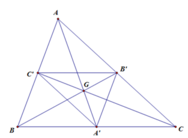
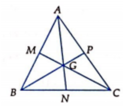
Ta có: D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB
Do đó: DE, EF, FD là các đường trung bình của tam giác ABC
Suy ra F E //= 1 2 B C D E //= 1 2 A B D F //= 1 2 A C
Do đó ta có các phép tịnh tiến như sau: T 1 2 B C → F = E ; T D E → B = F
Lại có G là trọng tâm tam giác ABC nên ta có DG = 1/2GA
T 1 2 G A → D = G ; T 2 D G → G = A
Vậy đáp án A, B, D đúng và C sai.
Chọn đáp án C.

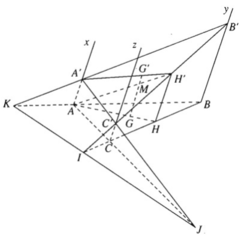
a) CC′ // BB′ ⇒ ΔICC′ ∼ ΔIBB′
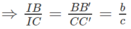
CC′ // AA′ ⇒ ΔJCC′ ∼ ΔJAA′
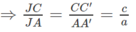
AA′ // BB′ ⇒ ΔKAA′ ∼ ΔKBB′
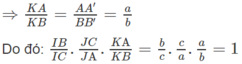
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH′ // BB′.
Mà BB′ // AA′ suy ra HH′ // AA′
Ta có: G ∈ AH và G′ ∈ A′H′ và ta có:
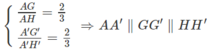
c) AH′ ∩ GG′ = M ⇒ GG′ = G′M + MG
Ta có: G′M // AA′ ⇒ ΔH′G′M ∼ ΔH′A′A
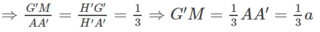
MG // HH′ ⇒ ΔAMG ∼ ΔAH′H
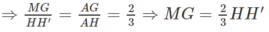
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên
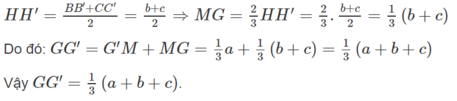

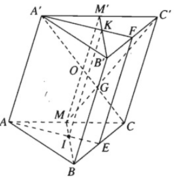
Gọi M và M’ tương ứng là trung điểm của AC và A’C’, ta có:
I ∈ BM, G ∈ C′M, K ∈ B′M′
Theo tính chất trọng tâm của tam giác ta có:
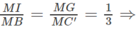
Ta có :
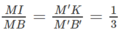
Mặt khác IG và IK ⊂ (IGK) nên (IGK) // (BB′C′C)
b) Gọi E và F tương ứng là trung điểm của BC và B’C’, O là trung điểm của A’C. A, I, E thẳng hàng nên (AIB’) chính là (AEB’). A’, G, C thẳng hàng nên (A’GK) chính là (A’CF).
Ta có B′E // CF (do B’FCE là hình bình hành ) và AE // A′F nên (AIB′) // (A′GK).
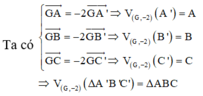
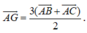
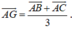
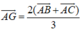
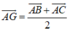
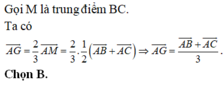
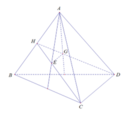
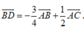

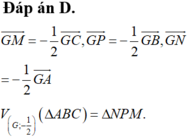
Do G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’ nên
Đáp án D