Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{8a^2+b}{4a}+b^2=2a+\frac{b}{4a}+b^2=a+a+\frac{b}{4a}+b^2\)
\(\ge a+1-b+\frac{1-a}{4a}+b^2=a+1-b+\frac{1}{4a}-\frac{1}{4}+b^2\)(do \(a+b\ge1\))
\(=\left(a+\frac{1}{4a}\right)+b^2-b+\frac{1}{4}+\frac{1}{2}\)
\(\ge2\sqrt{a\cdot\frac{1}{4a}}+\left(b-\frac{1}{2}\right)^2+\frac{1}{2}\)
\(\ge2\cdot\frac{1}{2}+\frac{1}{2}=\frac{3}{2}\)
Dấu = khi \(a=b=\frac{1}{2}\)

Áp dụng bất đẳng thức Cosi ta có :
\(4\ge a+b\ge2\sqrt{ab}\Leftrightarrow\sqrt{ab}\le2\Leftrightarrow ab\le4\)
Ta có bất đẳng thức \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
(Nhân chéo để chứng minh )
Áp dụng :
\(S=\frac{1}{a^2+b^2}+\frac{25}{ab}+ab=\frac{1}{a^2+b^2}+\frac{1}{2ab}+\frac{49}{2ab}+ab\)
\(=\frac{1}{a^2+b^2}+\frac{1}{2ab}+ab+\frac{16}{ab}+\frac{17}{2ab}\)
\(\ge\frac{4}{a^2+b^2+2ab}+2\sqrt{ab.\frac{16}{ab}}+\frac{17}{2ab}\)
\(\ge\frac{4}{\left(a+b\right)^2}+8+\frac{17}{2.4}=\frac{1}{4}+8+\frac{17}{8}=\frac{83}{8}\)
Dấu " = " xảy ra \(\Leftrightarrow a=b=2\)

đặt \(t=ab+bc+ca\)
\(=>t=ab+bc+ca\le\frac{1}{3}\left(a+b+c\right)^2=3\)
mặt khác
\(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ca\right)\)
\(=>a^2+b^2+c^2=9-2\left(ab+bc+ca\right)\)
khi đó
\(P=\frac{9-2t}{t}\)(zới t nhỏ hơn hoặc = 3)
xét \(f\left(t\right)=\frac{9-2t}{t}\left(t\le3\right)\)
\(f'\left(t\right)=-\frac{9}{t^2}< 0\)
=> f(t) N Biến \(\left(-\infty,3\right)\)
min f(t)=f(3)=1
koo tồn tại max\(f\left(t\right)\)
zậy minP=1 khi a=b=c=1

\(S=\frac{1}{a^2+b^2}+\frac{25}{ab}+ab\)
\(=\left(\frac{1}{a^2+b^2}+\frac{1}{2ab}\right)+\left(ab+\frac{16}{ab}\right)+\frac{17}{2ab}\)
\(\ge\frac{4}{\left(a+b\right)^2}+2\sqrt{ab\cdot\frac{16}{ab}}+\frac{17}{\frac{\left(a+b\right)^2}{2}}\)
\(\ge\frac{4}{4^2}+8+\frac{17}{\frac{4^2}{2}}=\frac{83}{8}\)
Dấu "=" xảy râ khi x = y = 2
Ta có \(a+b\ge2\sqrt{ab}\)=> \(ab\le4\)
\(\frac{1}{a^2+b^2}+\frac{1}{2ab}\ge\frac{4}{\left(a+b\right)^2}\ge\frac{1}{4}\)
\(\frac{16}{ab}+ab\ge8\)
\(\frac{17}{2ab}\ge\frac{17}{8}\)
=> \(S\ge8+\frac{17}{8}+\frac{1}{4}=\frac{83}{8}\)
Vậy MinS=83/8 khi a=b=2
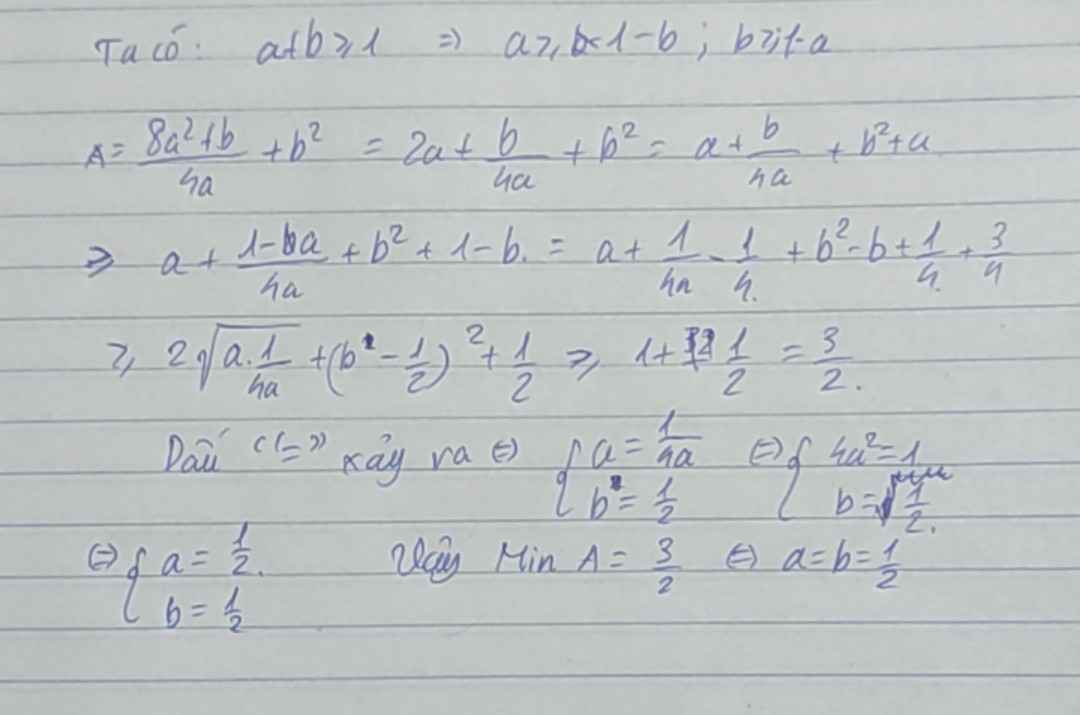
\(N=\frac{\left(a-b\right)^2+2ab+1}{a-b}=\frac{\left(a-b\right)^2+9}{a-b}=a-b+\frac{9}{a-b}\ge2\sqrt{\frac{9\left(a-b\right)}{a-b}}=6\)
\(N_{min}=6\) khi \(\left\{{}\begin{matrix}a-b=3\\ab=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=4\\b=1\end{matrix}\right.\)