Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ \(\frac{a^2+b^2}{a-2b}=2\Rightarrow a^2+b^2=2\left(a-2b\right)\)
\(\Leftrightarrow a^2+b^2=2a-4b\)
\(\Leftrightarrow a^2+b^2+4b=2a\)
\(\Leftrightarrow a.a+b.b+4b=2.a\)
\(\Leftrightarrow a.a+b\left(b+4\right)=2.a\)
\(\Leftrightarrow2.a-a.a=b\left(b+4\right)\)
\(\Leftrightarrow\frac{a}{b}=\frac{b+4}{2-a}\)
Mà muốn P lớn nhất thì a,b phải lớn nhất \(\Rightarrow a=b+4;b=2-a\)
\(\Leftrightarrow a+b=2\Leftrightarrow b+4+b=2\Leftrightarrow2b=-2\Rightarrow b=-1;a=3\)
\(\Rightarrow P=8a+4b=24-4=20\)
Cho hai số a,b thoả mãn a\(a^2+b^2=4a+2b+540\)Tính gía trị lớn nhất của biểu thức P= \(23a+4b+2013\)

ta có:a^2+b^2=4a+2b+540
<=>(a-2)^2+(b-1)^2=545
ta có:P=23a+4b+2013=23(a-2)+4(b-1)+2063
áp dụng bdt Bu-nhi-a-cốp-ski ta có:
(23(a-2)+4(b-1))^2nho hơn hoặc bằng (23^2+4^2)((a-2)^2+(b-1)^2)=545.545=545^2
=>23(a-2)+4(b-1) nhỏ hơn hoặc bằng 545
=>P nhỏ hơn hoặc bằng 545+2063=2608.dấu bằng xảy ra khi a=25;b=5
vậy maxP=2608 tại a=25;b=5

\(a+\frac{1}{b}\le1=>ab+1\le b\)
\(b\le ab+1\ge2\sqrt{ab}=>\sqrt{b}\ge2\sqrt{a}=>\frac{b}{a}\ge4\)
\(T=\frac{ab}{a^2+b^2}=\frac{1}{\frac{a}{b}+\frac{b}{a}}=\frac{1}{\frac{a}{b}+\frac{b}{16a}+\frac{15b}{16a}}\)
áp dụng cô si
\(\frac{a}{b}+\frac{b}{16a}\ge2\sqrt{\frac{ab}{16ab}}=\frac{1}{2}=>T\le\frac{1}{\frac{1}{2}+\frac{15}{16}.4}=\frac{4}{17}\)
\(=>MaxT=\frac{4}{17}\)
dấu = xảy ra khi
\(b=4a;\frac{a}{b}=\frac{b}{16a};ab=1\)
\(=>\hept{\begin{cases}4a^2=1\\b=4a\end{cases}=>\hept{\begin{cases}a=\frac{1}{2}\\b=2\end{cases}}}\)
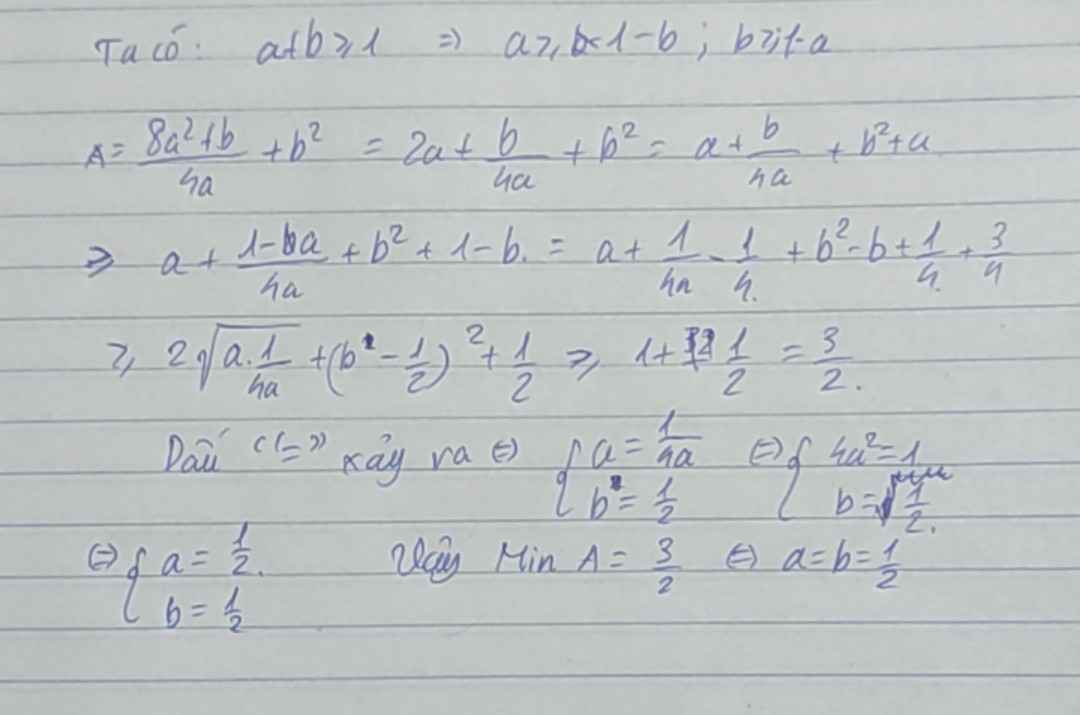
Ta có: \(b=0,25P-2a\) thế ngược lên trên ta được
\(\frac{a^2+\left(0,25P-2a\right)^2}{a-2\left(0,25P-2a\right)}=2\)
\(\Leftrightarrow80a^2-a\left(16P+160\right)+P^2+16P=0\)
Để PT có nghiệm thì:
\(\Delta'\ge0\)
Làm tiếp nhé
bạn cx thi violympic ak