
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án A
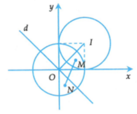

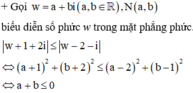
=> Tập hợp các điểm M là nửa mặt phẳng không chứa điểm I(1;1), có bờ là đường thẳng x + y = 0 (d)


Theo hệ quả của bất đẳng thức Cauchy - Schwarz
\(\Rightarrow x^2+y^2+z^2\ge xy+yz+xz\)
Mà \(x^2+y^2+z^2\le3\)
\(\Rightarrow xy+yz+xz\le3\)
Ta có \(P=\dfrac{1}{1+xy}+\dfrac{1}{1+yz}+\dfrac{1}{1+xz}\)
Áp dụng bất đẳng thức Cauchy - Schwarz dạng phân thức
\(\Rightarrow P\ge\dfrac{\left(1+1+1\right)^2}{xy+1+yz+1+xz+1}=\dfrac{9}{xy+yz+xz+3}\) (1)
Ta có \(xy+yz+xz\le3\)
\(\Rightarrow xy+yz+xz+3\le6\)
\(\Rightarrow\dfrac{9}{xy+yz+xz+3}\ge\dfrac{9}{6}=\dfrac{3}{2}\) (2)
Từ (1) và (2)
\(\Rightarrow P\ge\dfrac{3}{2}\)
Vậy \(P_{min}=\dfrac{3}{2}\)
Dấu " = " xảy ra khi \(x=y=z=1\)

Đặt z = a + bi với a , b ∈ R
Khi đó
z - 2 i z - 2 = a + b - 2 i a - 2 + b i = a + b - 2 i a - 2 - b i a - 2 2 + b 2 = a a - 2 + b b - 2 a - 2 2 + b 2 + a - 2 b - 2 - a b a - 2 2 + b 2
z - 2 i z - 2 là số ảo khi và chỉ khi
a a - 2 + b b - 2 a - 2 2 + b 2 = 0 ⇔ a 2 + b 2 = 2 a + b a - 2 2 + b 2 ≠ 0
Ta có
P = z - 1 + z - i = a - 1 + b i + a + b - 1 i = a - 1 2 + b + a 2 + b - 1 2 = a 2 + b 2 - 2 a + 1 + a 2 + b 2 - 2 b + 1 = 2 a + b - 2 a + 1 + 1 a + b - 2 a + 1 = 1 + 2 b + 1 + 2
Áp dụng bất đẳng thức Cauchy ta có: 2 a + b = a 2 + b 2 ≥ 1 2 a + b 2
Suy ra a + b ≤ 4
Do đó P 2 ≤ 2 2 + 2 a + b ≤ 20 ⇔ P ≤ 2 5
Dấu “=” xảy ra khi và chỉ khi a = b = 2
Vậy maxP = 2 5 đạt được khi z = 2 + 2i
Đáp án C

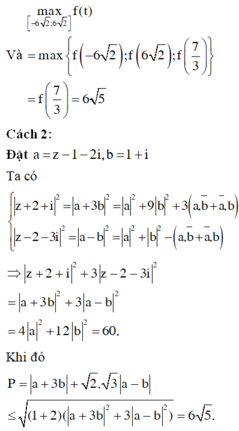


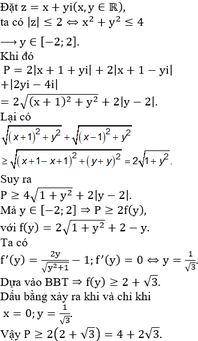


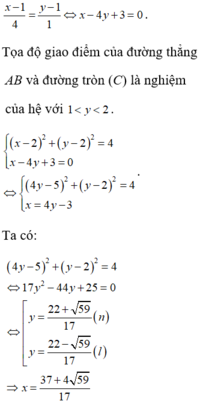
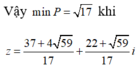
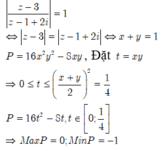
Đáp án C.
Ta có 1 = z 1 - z 2 z 1 - z 2 = z 1 - z 2 z 1 - z 2 ¯ = z 1 2 + z 2 2 - z 1 z 2 + z 2 z 1 ⇔ z 1 z 2 + z 2 z 1 = 1 P = z 1 z 2 2 + z 2 z 1 2 = z 1 z 2 + z 2 z 1 2 - 2 = z 1 z 2 z 2 2 + z 2 z 1 z 1 2 2 - 2 = z 1 z 2 + z 2 z 1 2 - 2 = - 1 . .