Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Δ=(a-2)^2-4(a^2-2a)
=-3a^2+4a+4
Để phương trình có hai nghiệm phân biệt thì -3a^2+4a+4<>0
=>a<>2 và a<>-2/3
|z1-z2|=|z1+z2|
=>(z1-z2)^2=(z1+z2)^2
=>z1z2=0
=>a^2-2a=0
=>a=0(nhận) hoặc a=2(loại)
=>Có 1 giá trị
Giải giúp mình bài này luôn với ạ
https://hoc24.vn/cau-hoi/1-trong-mat-phang-toa-do-oxy-cho-hai-diem-a02-b42-tim-diem-m-tren-doan-thang-ab-de-parabol-p-dinh-o-va-di-qua-diem-m-chia-tam-giac-vuong-oab-thanh-hai-phan-co-dien-tich-bang-nhau2-cho-h.7896187554129
Đáp án A
Phương trình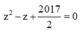 
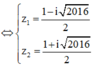
Ta có 
Vật giá trị nhỏ nhất của biểu thức P là 
Đáp án A
Phương pháp.
Giả sử 
Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa 
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm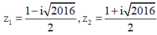 
Giả sử 
. Từ 
ta suy ra
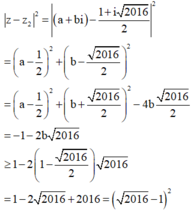
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của 
là
2016
-
1
Đạt được khi và chỉ khi 
Nếu z = a + bi thì z + z = 2a ∈ R; z. z = a 2 + b 2 ∈ R
z và z là hai nghiệm của phương trình (x − z)(x − z ) = 0
⇔ x 2 − (z + z ) x + z. z = 0
⇔ x 2 − 2ax + a 2 + b 2 = 0
Nếu z = a + bi thì z + z = 2a ∈ R; z. z = a 2 + b 2 ∈ R
z và z là hai nghiệm của phương trình (x − z)(x − z ) = 0
⇔ x 2 − (z + z ) x + z. z = 0
⇔ x 2 − 2ax + a 2 + b 2 = 0
Chọn C.
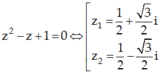
Ta có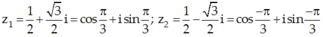 
Áp dụng công thức Moa-vrơ:
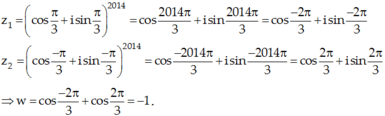
Phần thực của w là -1, phần ảo là 0.
