
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tóm tắt: \(F_1=F_2=20N\)\(;F_{hl}=20N\)
\(\alpha=?\)
Bài giải:
Gọi góc giữa hai lực này là \(\alpha\)
Ta có: \(F^2=F_1^2+F_2^2+2F_1\cdot F_2\cdot cos\alpha\)
\(\Rightarrow cos\alpha=\dfrac{F^2-F_1^2-F_2^2}{2\cdot F_1\cdot F_2}=\dfrac{20^2-20^2-20^2}{2\cdot20\cdot20}=-\dfrac{1}{2}\)
\(\Rightarrow\alpha=120^o\)
Chọn D.

Chọn D.
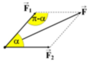
Theo định lý hàm số cosin:
F 2 = F 1 2 + F 2 2 - 2 F 1 F 2 cos ( π - α )
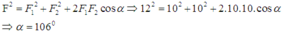

1.
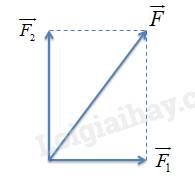
Ta thấy: \({10^2} = \sqrt {{6^2} + {8^2}} \Rightarrow {F^2} = \sqrt {F_1^2 + F_2^2} \)
Suy ra \({F_1} \bot {F_2}\)
2.
a)
Biểu diễn các lực kéo của mỗi tàu và hợp lực tác dụng vào tàu chở hàng:
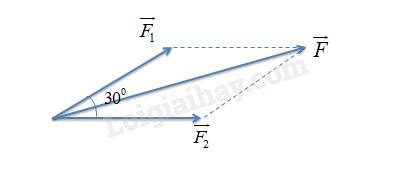
b)
Độ lớn của hợp lực là:
\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \left( {{F_1},{F_2}} \right)} \)
\( \Leftrightarrow F = \sqrt {{{8000}^2} + {{8000}^2} + 2.8000.8000.\cos {{30}^0}} \)
\( \Leftrightarrow F = 15455\left( N \right)\)
c)
Hợp lực có:
- Chiều: hướng về phía trước
- Phương: hợp với \(\overrightarrow {{F_1}} \) góc \({15^0}\)
d) Nếu góc giữa hai dây cáp bằng \({90^0}\) thì hợp lực có:
- Phương: xiên
- Chiều hướng sang trái hoặc phải.
- Độ lớn: \(F = \sqrt {F_1^2 + F_2^2} \)

Hai lực đồng quy có cùng độ lớn nên hợp lực F = 2F1.cos (α/2)
=> cos(α/2) = \(\frac{F}{F_1}\) = 1/2
=> α/2 = 600
=> α = 1200
Chúc bạn học tốt!!!