Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

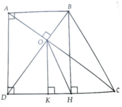
a, Tính được DB=15cm. A D B ^ ≈ 37 0 ; A B D ^ ≈ 53 0
b, Tính được AO=7,2cm, DO=9,6cm và AC=20cm
c, Kẻ OK ⊥ DC tại K
DH=AB=9cm, DC=16cm, DK=5,76cm và OK=7,68cm
Từ đó S D O H = O K . D H 2 = 7 , 68 . 9 2 = 34,56 c m 2

Câu 11.12.
Kẻ đường cao \(AH,BK\).
Do tam giác \(\Delta AHD=\Delta BKC\left(ch-gn\right)\)nên \(DH=BK\).
Đặt \(AB=AH=x\left(cm\right),x>0\).
Suy ra \(DH=\frac{10-x}{2}\left(cm\right)\)
Xét tam giác \(AHD\)vuông tại \(H\):
\(AD^2=AH^2+HD^2=x^2+\left(\frac{10-x}{2}\right)^2\)(định lí Pythagore)
Xét tam giác \(DAC\)vuông tại \(A\)đường cao \(AH\):
\(AD^2=DH.DC=10.\left(\frac{10-x}{2}\right)\)
Suy ra \(x^2+\left(\frac{10-x}{2}\right)^2=10.\frac{10-x}{2}\)
\(\Leftrightarrow x=2\sqrt{5}\)(vì \(x>0\))
Vậy đường cao của hình thang là \(2\sqrt{5}cm\).
Câu 11.11.
Kẻ \(AE\perp AC,E\in CD\).
Khi đó \(AE//BD,AB//DE\)nên \(ABDE\)là hình bình hành.
Suy ra \(AE=BD=15\left(cm\right)\).
Kẻ đường cao \(AH\perp CD\)suy ra \(AH=12\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AH\):
\(\frac{1}{AH^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AE^2}=\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AC=20\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.15.20=150\left(cm^2\right)\),

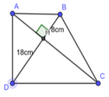
Xét ∆ ADB vuông tại A có: AH là đường cao ứng với cạnh huyền BD
⇒ A H 2 = HB. HD = 8.18 HA = 12 (cm) (hệ thức lượng trong tam giác vuông)
Xét ∆ ADC vuông tại D có: DH là đường cao ứng với cạnh huyền AC
⇒ H D 2 = H A . H C ⇒ 18 2 = 12 H C => HC = 27 (cm) (hệ thức lượng trong tam giác vuông)
Ta có: AC = AH + HC = 12 + 27 = 39 cm
BD = BH + HD = 8 + 18 = 26cm
S A B C D = A C . B D 2 = 26.39 2 = 507 c m 2
Đáp án cần chọn là: D
Bài giải : Diện tích tam giác ABD là:
(12 x (12 : 2))/2 = 36 (cm2)
Diện tích hình vuông ABCD là:
36 x 2 = 72 (cm2)
Diện tích hình vuông AEOK là:
72 : 4 = 18 (cm2)
Do đó : OE x OK = 18 (cm2)
r x r = 18 (cm2)
Diện tích hình tròn tâm O là:
18 x 3,14 = 56,92 (cm2)
Diện tích tam giác MON = r x r : 2 = 18 : 2 = 9 (cm2)
Diện tích hình vuông MNPQ là:
9 x 4 = 36 (cm2)
Vậy diện tích phần gạch chéo là:
56,52 - 36 = 20,52 (cm2)
Bài giải : Diện tích tam giác ABD là:
(12 x (12 : 2))/2 = 36 (cm2)
Diện tích hình vuông ABCD là:
36 x 2 = 72 (cm2)
Diện tích hình vuông AEOK là:
72 : 4 = 18 (cm2)
Do đó : OE x OK = 18 (cm2)
r x r = 18 (cm2)
Diện tích hình tròn tâm O là:
18 x 3,14 = 56,92 (cm2)
Diện tích tam giác MON = r x r : 2 = 18 : 2 = 9 (cm2)
Diện tích hình vuông MNPQ là:
9 x 4 = 36 (cm2)
Vậy diện tích phần gạch chéo là:
56,52 - 36 = 20,52 (cm2)