Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
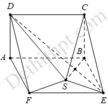
Vì S đối xứng với B qua
D E ⇒ d B ; D C E F = d S ; D C E E F .
Gọi M là trung điểm
C E ⇒ B M ⊥ D C E F ⇒ d B ; D C E F = B M .
Khi đó, thể tích V A B C D S E F = V A D F . B C E + V S . D C E F
= A B x S Δ A D F + 1 3 d S ; D C E F x S D C E F = 1. 1 2 + 1 3 . 2 2 . 2 = 1 2 + 1 3 = 5 6 .

Chọn đáp án C
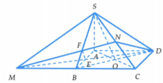
Gọi O là giao điểm của AC và BD
Ta có
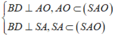
![]()
![]()
⇒ Thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (MND) là tứ giác DEFN.
Suy ra V 1 = V S . A D E F N và V 2 = V B C D E F N
Từ giả thiết ta có ∆ A B D đều cạnh a
![]()
Thể tích khối chóp N.MCD là
V N . M C D = 1 3 d N ; M C D . S ∆ M C D = a 3 4
Ta có F là trọng tâm của ∆ S M C nên M F M N = 2 3 ; E là trung điểm của MD nên M E M D = 1 2
Áp dụng công thức tính thể tích ta có:
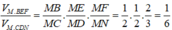
![]()
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 . S A . S A B C D = a 3 4
Suy ra V 1 = V S . A D E F N = V S . A B C D - V 2 = a 3 24
Vậy V 1 V 2 = 1 5

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m
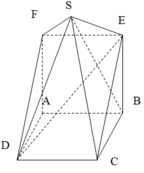
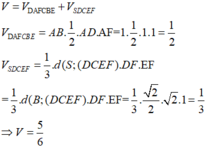
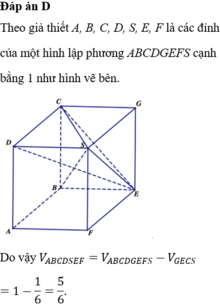

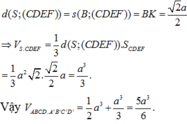
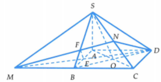

Ta tách khối đa diện thành hai phần.
Phần 1. Lăng trụ tam giác DAF.CBE có V = 1 2
Phần 2. Hình chóp tam giác S.CEFD có
V S . C D F D = V B . C E F D = 2 3 V D A F . C B E = 1 3 ⇒ V A B C D E F = 5 6
Đáp án cần chọn là D