Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: AD // BC (ABCD là hình bình hành)
Mà AD thuộc (AFD), BC thuộc (BEC)
Nên (AFD) // (BEC)
b) Trong (ABEF) kẻ đường thẳng d qua M // AF
Ta có: d cắt AB tại I, d cắt EF tại J (1)
Trong (ABCD) có I thuộc (P) mà (P) // (AFD)
Suy ra từ I kẻ IH // AD (2)
(1)(2) suy ra (IJH) trùng (P) và // (AFD)
Ta có: (P) cắt AC tại N mà AC thuộc (ABCD), IH thuộc (P) và (ABCD)
Suy ra: IH cắt AC tại N
Ta có các hình bình hành IBCH, IBEJ
Gọi O là trung điểm của AB
Có M là trọng tâm △ABE
Suy ra: \(\dfrac{MO}{ME}=\dfrac{1}{2}\).
Ta có: AB // CD suy ra: AI // CH
Định lí Ta-lét: \(\dfrac{AN}{NC}=\dfrac{AI}{CH}\)
mà CH = IB (IBCH là hình bình hành)
Suy ra: \(\dfrac{AN}{NC}=\dfrac{AI}{IB}\)
Ta có: AB // EF nên OI // EJ
Do đó: \(\dfrac{OI}{EJ}=\dfrac{MO}{ME}=\dfrac{1}{2}\)
Mà EJ = IB (IBEJ là hình bình hành)
Suy ra: \(\dfrac{OI}{IB}=\dfrac{1}{2}\) hay IB = 2OI
Ta có: \(\dfrac{AN}{NC}=\dfrac{AI}{IB}=\dfrac{AO+OI}{2OI}\)
Mà OA = OB (O là trung điểm AB)
Nên \(\dfrac{AN}{NC}=2\).

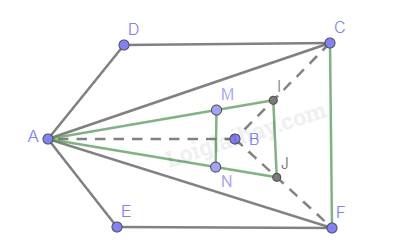
Gọi I,J lần lượt là trung điểm của BC, BF
Suy ra, IJ là đường trung bình của tam giác BCF.
Do đó, IJ // CF (1)
Tam giác AIJ có: \(\frac{{AM}}{{AI}} =\frac{{AN}}{{AJ}}= \frac{2}{3}\)
Suy ra, MN // IJ (theo Ta lét) (2)
Từ (1) và (2) suy ra MN // CF, mà CF nằm trong (ACF).
Suy ra MN // (ACF)

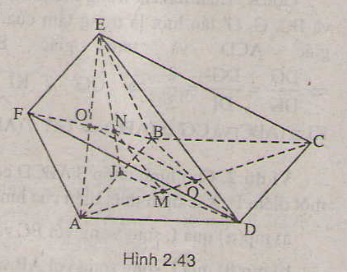
a) Do các tứ giác ABCD và ABEF là các hình bình hành
=> O là trung điểm của AC và BD
và O’ là trung điểm của AE và BF. (tính chất hình bình hành).
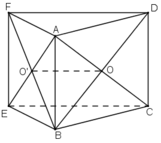
+ ΔBFD có OO’ là đường trung bình nên OO’ // DF
mà DF ⊂ (ADF)
⇒ OO' // (ADF)
+ ΔAEC có OO’ là đường trung bình nên OO’ // EC
mà EC ⊂ (BCE)
⇒ OO’ // (BCE).
b)
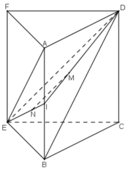
Ta thấy mp(CEF) chính là mp(CEFD).
Gọi I là trung điểm của AB:
+ M là trọng tâm ΔABD
⇒ IM/ ID = 1/3.
+ N là trọng tâm ΔABE
⇒ IN/IE = 1/3.
+ ΔIDE có IM/ID = IN/IE = 1/3
⇒ MN // DE mà ED ⊂ (CEFD)
nên MN // (CEFD) hay MN // (CEF).

a) OO' là đường trung bình của tam giác DBF nên OO' // DF.
DF nằm trong mặt phẳng (ADF) nên OO' // mp(ADF).
Tương tự OO' // CE mà CE nằm trong mặt phẳng (BCE) nên OO' // mp(BCE).
b) Gọi J là trung điểm đoạn thẳng AB, theo định lí Ta-lét \(\Rightarrow\) MN // DE => đpcm.

Đáp án C
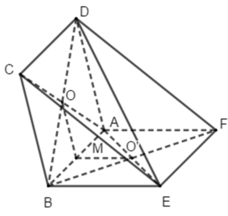
+) Ta có: BC // AD; BE // AF (ABCD và ABEF là hình bình hành)
Suy ra BC // (ADF); BE // (ADF)
Mà BC ∩ BE = B
Do đó (ADF) // (BEC).
+) O và O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O và O’ là trung điểm của BF và BD
Xét tam giác ABF có MO’ là đường trung bình nên MO’ // AF
MO’ // (ADF) (1)
Tương tự MO là đường trung bình của tam giác ABD nên MO // AD
MO // (ADF) (2)
Từ (1) và (2) suy ra (MOO’) // (ADF)
+) Chứng minh tương tự ta cũng có (MOO’) // (BCE).
+) Hai mặt phẳng (AEC) và (BDF) có:
AC ∩ DB = O ; AE ∩ BF = O’
Suy ra (AEC) ∩ (BDF) = OO’.
Vậy khẳng định (I); (II); (III) đúng.

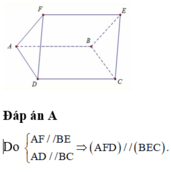

Phương án A sai vì AD và (BEF) cắt nhau tại A.
Phương án B đúng vì AD // BC, AF // BE
Phương án C sai vì (ABD) và (EFC) có điểm C chung
Đáp án B