Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) đây nha : https://hoc24.vn/hoi-dap/question/637285.html
câu 2 cũng chả khác gì cả

Giả sử G là trọng tâm tam giác ABC, ta sẽ chứng minh G' cũng là trọng tâm tam giác A'B'C'.
G là trọng tâm tam giác ABC nên: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
Ta cần chứng minh: \(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=\overrightarrow{0}\).
Theo giả thiết:
\(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AG}+\overrightarrow{GA'}+\overrightarrow{BG}+\overrightarrow{GB'}+\overrightarrow{CG}+\overrightarrow{GC'}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}+\left(\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}-\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}-\overrightarrow{0}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=\overrightarrow{0}\)
Vậy G là trọng tâm tam giác A'B'C' hay hai tam giác ABC và A'B'C' có cùng trọng tâm.

Các kí hiệu bên dưới đều là vecto chứ ko phải đoạn thẳng:
a/ \(BB'+CC'+BA+CA=2AA'+BA+CA\)
\(=2\left(AB+BA'\right)+BA+CA=2AB+2BA'+BA+CA\)
\(=AB+CA+2BA'=CB+2BA'=CA'+A'B+2BA'\)
\(=BA'+CA'\)
b/ \(AA'+BB'+CC'=AB+BA'+BC+CB'+CA+AC'\)
\(=AB+BC+CA+BA'+CB'+AC'\)
\(=AC+CA+BA'+CB'+AC'\)
\(=BA'+CB'+AC'\)

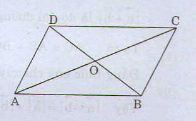
Do là giao điểm của hai đường chéo hình bình hành nên:
\(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\)\(=\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}\)
\(=4\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\)
\(=4\overrightarrow{MO}\) (ĐPCM).

A B D C O / / // // a) Chứng minh \(\overrightarrow{AC}-\overrightarrow{BA}=\overrightarrow{AD}\)
Ta có: \(\overrightarrow{AC}-\overrightarrow{CD}=\overrightarrow{AD}\left(đpcm\right)\) ( vì \(\overrightarrow{BA}=\overrightarrow{CD}\) )
b) Chứng minh \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=AC\)
Ta có: \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\) ( theo quy tắc hình bình hành )
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC\left(đpcm\right)\)
bài này chả khó áp dụng 1 bước là ra ngay điều cần chứng minh rồi

A B C D O
a) \(\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{DO}=\left(\overrightarrow{AO}+\overrightarrow{CO}\right)+\left(\overrightarrow{BO}+\overrightarrow{DO}\right)\)
\(=\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\).
b) \(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}=\overrightarrow{AC}+\overrightarrow{AC}=2\overrightarrow{AC}\).
c) \(\overrightarrow{OC}-\overrightarrow{OD}=\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{DC}\).

\(\overrightarrow{AA'}=\overrightarrow{AO}+\overrightarrow{OO'}+\overrightarrow{O'A'}\)
Tách tương tự với 3 số hạng còn lại sau đó cộng vế với vế và chú ý rằng: \(\overrightarrow{AO}+\overrightarrow{CO}=\overrightarrow{0};\) \(\overrightarrow{BO}+\overrightarrow{DO}=\overrightarrow{0}\); \(\overrightarrow{O'A'}+\overrightarrow{O'C'}=\overrightarrow{0}\) ; \(\overrightarrow{O'B'}+\overrightarrow{O'D'}=\overrightarrow{0}\) theo tính chất hình bình hành ta sẽ có đpcm