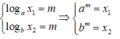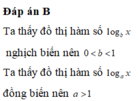
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
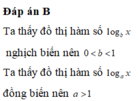
Chọn A
Đồ thị của hàm số 
liên tục trên các đoạn 
và 
, lại có 
là một nguyên hàm của 
.
Do đó diện tích của hình phẳng giới hạn bởi các đường:
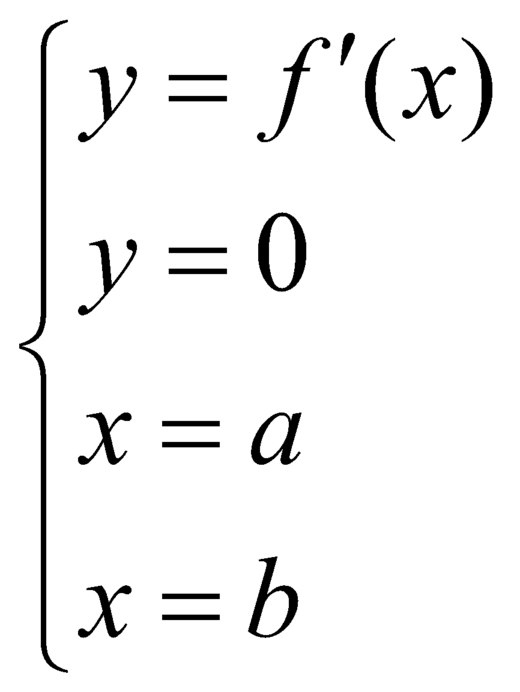là:
.
Vì 
Tương tự: diện tích của hình phẳng
giới hạn bởi các đường: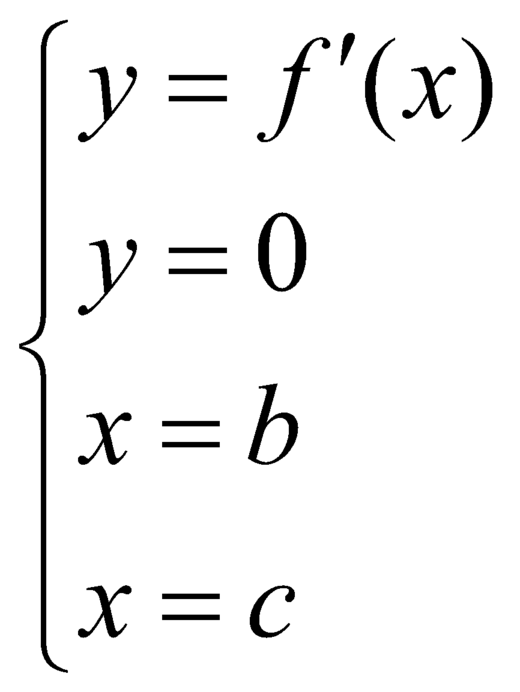 
là:
.
.
Mặt khác, dựa vào hình vẽ ta có: 
.
Từ (1), (2) và (3) ta chọn đáp án A.
( có thể so sánh 
với 
dựa vào dấu của 
trên đoạn 
và so sánh 
với 
dựa vào dấu của 
trên đoạn 
)
Đáp án D
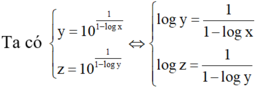
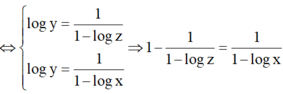
⇔ log z - 1 log z = 1 1 - log x
⇔ 1 - log x = log z log z - 1
⇔ log x = - 1 log z - 1 ⇔ x = 10 1 1 - log z .
Chọn C
+ ta có: f’( x) = 0 khi x= -1 hoặc x= -2.
+ Giá trị của hàm số y= f’(x) không đổi dấu khi đi qua x= - 1 nên x= -1 không là điểm cực trị của hàm số.
+ Giá trị của hàm số y= f’(x) đổi dấu từ âm sang dương khi qua x= -2
=> Hàm số y= f(x) đạt cực tiểu tại điểm x= -2.
Chọn A
Do y = logax và y = logbx là hai hàm đồng biến nên a > 1; b > 1
Do y = logcx nghịch biến nên c < 1 . Vậy c bé nhất.
Mặt khác: Lấy y = m, khi đó tồn tại x1; x2 > 0 để
