Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hoành độ giao điểm thỏa mãn pt
\(\left(k-\frac{2}{3}\right)x+1=\left(2-k\right)x-3\)
\(\Leftrightarrow kx-\frac{2}{3}x+1=2x-xk-3\Leftrightarrow2xk-\frac{8}{3}x+4=0\)
Thay x = 4 vào pt trên ta được :
\(8k-\frac{32}{3}+4=0\Leftrightarrow k=\frac{5}{6}\)
với x=-3 ta có tung độ tương ứng của đường thẳng thứ nhất là :
\(y_1=\left(5k+2\right).\left(-3\right)-3=-15k-9\)
tương tự ta có \(y_2=\left(3k-2\right).\left(-3\right)+2=-9k+8\)
để hai đường thẳng cắt nhau tại điểm có hoành độ bằng -3 thì
\(y_1=y_2\Leftrightarrow-15k-9=-9k+8\Leftrightarrow k=-\frac{17}{6}\)
Tọa độ giao điểm của \(y=-2x+k\) và trục hoành: \(y=0\Rightarrow x=\dfrac{k}{2}\)
Tọa độ giao điểm \(y=-2x+k\) với trục tung: \(x=0\Rightarrow y=k\)
Tọa độ giao điểm của \(y=3x-k+4\) với trục hoành: \(y=0\Rightarrow x=\dfrac{k-4}{3}\)
Tọa độ giao điểm của \(y=3x-k+4\) với trục tung: \(x=0\Rightarrow y=-k+4\)
a. Đồ thị các hàm cắt nhau tại 1 điểm trên trục tung khi:
\(k=-k+4\Rightarrow x=2\)
b. Đồ thị các hàm cắt nhau tại 1 điểm trên trục hoành khi:
\(\dfrac{k}{2}=\dfrac{k-4}{3}\Rightarrow k=-8\)
vẽ đồ thị hàm số y=/x/+4x . Với giá trị nào của k thì hàm số y=k cắt đồ thị hàm số trên tại hai điểm phân biệt
a, 2 đường thẳng // với nhau khi
\(\hept{\begin{cases}k+3=5-k\\2\ne3\end{cases}\Leftrightarrow k=1}\)
b, 2 đường thẳng cắt nhau khi
\(k+3\ne5-k\Leftrightarrow k\ne1\)
c, 2 đường thẳng trên ko thể trùng nhau được vì hệ số tự do 2 \(\ne\)3
Hàm số y = ( k + 1) x + 3 có các hệ số a = k + 1, b = 3
Hàm số y = ( 3 – 2k ) x + 1 có các hệ số a' = 3 - 2k, b' = 1
Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là :
\(k+1\ne0\)và \(3-2k\ne0\)hay \(k\ne-1\)và \(k\ne\frac{3}{2}\)( * )
b) Hai đường thẳng y = ( k + 1 ) x + 3 và y = ( 3 – 2k ) x + 1 là hàm số bậc nhất nên \(a\ne0\) và \(a'\ne0\) Hai đường thẳng này cắt nhau khi \(a\ne a'\) tức là :
\(\hept{\begin{cases}k+1\ne0\\3-2k\ne\\k+1\ne3-2k\end{cases}0}\Leftrightarrow\hept{\begin{cases}k\ne-1\\2k\ne\\3k\ne2\end{cases}3}\Leftrightarrow\hept{\begin{cases}k\ne-1\\k\ne\\k\ne\frac{2}{3}\end{cases}\frac{3}{2}}\)
Với \(k\ne-1 ; k\ne\frac{3}{2} ; k\ne\frac{2}{3}\) thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
c) Do \(b\ne b'\) ( vì \(3\ne1\) ) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.
Hàm số y = ( k + 1)x + 3 có các hệ số a = k + 1, b = 3
Hàm số y = (3 – 2k)x + 1 có các hệ số a' = 3 - 2k, b' = 1
Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là:
a) Theo đề bài ta có b ≠ b' (vì 3 ≠ 1)
Nên hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 song song với nhau khi a = a'
tức là: k + 1 = 3 – 2k
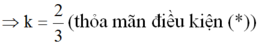
b) Hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 là hàm số bậc nhất nên a ≠ 0 và a' ≠ 0. Hai đường thẳng này cắt nhau khi a ≠ a' tức là:
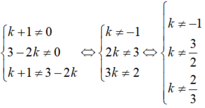
Vậy với 
thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
c) Do b ≠ b' (vì 3 ≠ 1) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.
b) Đồ thị hai hàm số y = (k + 3)x – 2 và y = (5 – k)x + 3 cắt nhau khi và chỉ khi:
k + 3 ≠ 5 - k ⇔ k ≠ 1
Kết hợp điều kiện với k ≠ 1; k ≠ -3 và k ≠ 5 thì đồ thị của hai hàm số đã cho cắt nhau.