Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình vẽ (Vào link là ra): https://i.imgur.com/GssTwiW.png
Ở đây mình sẽ cho R là bán kính của đường tròn O; R' là bán kính của đường tròn O'
a) ta có: \(\hept{\begin{cases}OM\perp MN\\O'N\perp MN\end{cases}}\)=> OM//O'N => \(\widehat{AOM}+\widehat{AO'N}=180^o\)
Xét ΔOAM có OM = OA (= R) => ΔOAM cân => \(\widehat{A_1}=\frac{180^o-\widehat{AOM}}{2}\left(1\right)\)
Xét ΔO'NA có O'N = O'A (=R') => ΔO'NA cân => \(\widehat{A_2}=\frac{180^o-\widehat{AO'N}}{2}\left(2\right)\)
\(\left(1\right)+\left(2\right)\Leftrightarrow\widehat{A_1}+\widehat{A_2}=\frac{180^o-\widehat{AOM}}{2}+\frac{180^o-\widehat{AO'N}}{2}.\)
\(=\frac{360^o-\left(\widehat{AOM}+\widehat{AO'N}\right)}{2}\)
\(=\frac{360^o-180^o}{2}=90^o.\)
\(\widehat{MAN}=180^o-\left(\widehat{A_1}+\widehat{A_2}\right)=180^o-90^o=90^o\)
=> ΔAMN vuông tại A
b) ta có: IM, IA là các tiếp tuyến của đường tròn (O) => IO là tia phân giác của \(\widehat{AIM}\)
IN; IA là các tiếp tuyến của đường tròn (O') => IO' là tia phân giác của \(\widehat{AIN}\)
do IO và IO' là hai tia phân giác của hai góc kề bù => \(IO\perp IO'\Rightarrow\widehat{OIO'}=90^o\)=> ΔIOO' là tam giác vuông.
c) Áp dụng hệ thức lượng trong ΔIOO', ta có: AI2 = OA . O'A = 8 x 4,5 = 36 => AI = 6(cm)
Xét ΔAMN vuông tại A, ta có: MN = 2AI = 2 x 6 = 12 (cm)
Đây là cách làm cùa mình. Nếu sai sót thì bình luận nhé!
Học tốt ^3^

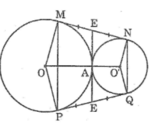
Ta có: MN ⊥ OM (tính chất tiếp tuyến)

Suy ra: QP ⊥ OP tại P
Vậy PQ là tiếp tuyến của đường tròn (O).
Ta có: MN ⊥ O’N (tính chất tiếp tuyến)

Suy ra: QP ⊥ O’Q tại Q

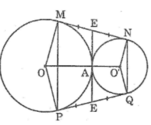
Kẻ tiếp tuyến chung tại A cắt MN tại E và PQ tại F
Trong đường tròn (O), theo tính chất hai tiếp tuyến cắt nhau, ta có:
EM = EA và FP = FA
Trong đường tròn (O’), theo tính chất hai tiếp tuyến cắt nhau, ta có:
EN = EA và FQ = FA
Suy ra: EM = EA = EN = (1/2).MN
FP = FA = FQ = (1/2).PQ
Suy ra : MN + PQ = 2EA + 2FA = 2(EA + FA) = 2EF (9)
Vì EF là đường trung bình của hình thang MNQP nên :
EF = (MP + NQ)/2 hay MP + NQ = 2EF (10)
Từ (9) và (10) suy ra: MN + PQ = MP + NQ