Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

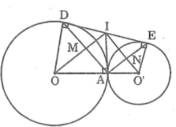
Ta có: IA = ID = IE (chứng minh trên)
Suy ra A nằm trên đường tròn tâm I đường kính DE
Vì OO’ ⊥ IA tại A nên OO’ là tiếp tuyến của đường tròn (I; DE/2)

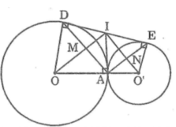
Tam giác AIO vuông tại A có AM ⊥ IO
Theo hệ thức lượng trong tam giác vuông, ta có: I A 2 = IM.IO (1)
Tam giác AIO’ vuông tại A có AN ⊥ IO’
Theo hệ thức lượng trong tam giác vuông, ta có: I A 2 = IN.IO’ (2)
Từ (1) và (2) suy ra: IM.IO = IN.IO’

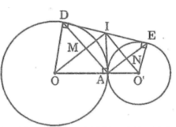
Tam giác O’IO vuông tại I có IA ⊥ OO’
Theo hệ thức lượng trong tam giác vuông, ta có:
I A 2 = OA.O’A = 5.3,2 = 16
Suy ra: IA = 4 (cm). Mà DE = 2IA nên DE = 2.4 = 8 (cm)

a) Xét (O): AI và DI là 2 tiếp tuyến cắt nhau tại I (gt)
=> AI = DI (TC 2 tiếp tuyến cắt nhau)
CMTT: AI = EI (TC 2 tiếp tuyến cắt nhau)
=> AI = EI = DI
Mà DE = EI + DI
=>AI = EI = DI =\(\dfrac{DE}{2}\)
Xét tam giác ADE có: AI = EI = DI =\(\dfrac{DE}{2}\)(cmt)
=> Tam giác ADE vuông tại A (định lý đảo đường trung tuyến trong tam giác vuông)
=> ^MAN = 90o
Xét tam giác AID: AI = DI (cmt) => Tam giác AID cân tại I
Mà IM là đường phân giác AID (AI và DI là 2 tiếp tuyến cắt nhau tại I)
=> IM là đường cao
=> ^IMA = 90o
CMTT: ^ANI = 90o
Xét TG AMIN:
^IMA = 90o (cmt)
^ANI = 90o (cmt)
^MAN = 90o (cmt)
=> AMIN là hình chữ nhật (dhnb)
b) Xét tam giác OAI vuông tại A, AM là đường cao ( do AM vg góc OI)
=> IM.IO = IA2 (HTL) (1)
Xét tam giác O'AI vuông tại A, AN là đường cao ( do AN vg góc O'I)
=> IN.IO' = IA2 (HTL) (2)
Từ (1) và (2) => IM.IO = IN.IO’ (đpcm)
c) Xét (O) và (O'): 2 đường tròn (O) và (O’) tiếp xúc ngoài tại A (cmt)
=> A \(\in\)OO' (TC đường nối tâm)
mà IA vg góc AO (do AI là tiếp tuyến trong của 2 đường tròn (O) và (O’) tiếp xúc ngoài tại A )
=> OO' vg góc AI tại A (*)
Xét tam giác ADE vuông tại A (^DAE = 90o do AMIN là hcn)
I là TĐ của DE (do ID = IE = \(\dfrac{DE}{2}\))
=> I là tâm đường tròn đường kính DE, nội tiếp tam giác ADE
=> A \(\in\)(I) (**)
Từ (*) và (**) => OO’ là tiếp tuyến của đường tròn đường kính DE có A là tiếp điểm.
d) Xét tg OIO' vuông tại I, AI là đường cao:
AI2 = AO . AO' (HTL)
=> AI2= R. R'
Mà AI = \(\dfrac{DE}{2}\)(cmt)
=> (\(\dfrac{DE}{2}\))2 = R . R'
<=> \(\dfrac{DE^2}{4}\) = R . R'
<=> DE = 2\(\sqrt{R.R'}\)

Trong đường tròn (O) ta có OI là tia phân giác của góc AID (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có O’I là tia phân giác của góc AIE (tính chất hai tiếp tuyến cắt nhau)
=> IO ⊥ IO’ (tính chất hai góc kề bù)
Suy ra =
90
°
hay
=
90
°
hay  =
90
°
=
90
°
Lại có: IA = ID (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác ADI cân tại I
Tam giác cân AID có IO là phân giác của góc AID nên IO cũng là đường cao của tam giác AID
Suy ra: IO ⊥ AD hay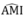 =
90
°
=
90
°
Mặt khác: IA = IE (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AEI cân tại I
Tam giác cân AIE có IO’ là phân giác của góc AIE nên IO’ cũng là đường cao của tam giác AIE
Suy ra: IO’ ⊥ AE hay =
90
°
=
90
°
Tứ giác AMIN có ba góc vuông nên nó là hình chữ nhật.