Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

http://lazi.vn/edu/exercise/cho-o-va-o-cat-nhau-o-a-va-b-o-va-o-thuoc-2-nua-mat-phang-bo-ab-mot-cat-tuyen-ke-qua-a-cat-o-o-c-va-cat-o

1.Cho (O;R). Qua điểm M nằm trong đương tròn vẽ các dây CD và EF không đi qua O. Tiếp tuyến tại C và D của (O) cắt nhau ở A, tiếp tuyến tại E và F của (O) cắt nhau tại B. Chứng minh OM vuông góc với AB
2. Cho (O) và đường thẳng d không cắt (O). Gọi H là hình chiếu của (O) trên d. Từ H vẽ các cát tuyến HCD và HAB với (O) (C nằm giữa H và D, A nằm giữa H và B, các cát tuyến không đi qua O). Tiếp tuyến tại A của (O) cắt d tại M. Tiếp tuyến tại C của (O) cắt d tại M. Chứng minh ΔOMN cân

a:góc OAD=góc OBD=90 độ
=>OBAD nội tiếp
b: góc EAO+góc ECO=180 độ
=>ECOA nội tiếp
=>góc OEC=góc OAC=góc ODB

1. Để chứng minh cung DE có số đo không đổi, ta cần chứng minh góc \(\angle BOC\) có số đo không đổi. Thực vậy, theo tính chất hai tiếp tuyến cắt nhau, OB và OC là phân giác ngoài của tam giác ABC. Ta có
\(\angle BOC=180^{\circ}-\frac{\angle MBC}{2}-\frac{\angle NCB}{2}=\frac{\angle ABC}{2}+\frac{\angle ACB}{2}=90^{\circ}-\frac{\angle BAC}{2}=90^{\circ}-\frac{a}{2}\)
Do đó góc \(\angle BOC\) có số đo không đổi. Suy ra cung DE có số đo không đổi.
2. Do CD vuông góc với AB nên BC,BD là đường kính của hai đường tròn (O) và (O'). Suy ra
\(\angle CFB=\angle DEB=90^{\circ}\to\angle CFD=\angle CED=90^{\circ}.\) Vậy tứ giác CDEF nội tiếp. Do đó \(\angle ECF=\angle EDF\to\angle FAB=\angle ECF=\angle EDF=\angle EDB\)
Vậy AB là phân giác của góc AEF.
3. Đề bài có chút nhầm lẫn, "kẻ \(IH\perp BC\) mới đúng. Do tam giác ABC nhọn và I nằm trong nên các điểm H,K,L nằm trên các cạnh của tam giác. Sử dụng bất đẳng thức \(a^2+b^2\ge\frac{1}{2}\left(a+b\right)^2,\) ta suy ra \(AL^2+BL^2\ge\frac{1}{2}\left(AL+BL\right)^2=\frac{1}{2}AB^2.\) Tương tự ta cũng có \(BH^2+CH^2\ge\frac{1}{2}BC^2,KC^2+KA^2\ge\frac{1}{2}AC^2.\) Mặt khác theo định lý Pitago
\(AL^2+BH^2+CK^2=\left(IA^2-IL^2\right)+\left(IB^2-IH^2\right)+\left(IC^2-IK^2\right)\)
\(=\left(IA^2-IK^2\right)+\left(IB^2-IL^2\right)+\left(IC^2-IH^2\right)\)
\(=BL^2+CH^2+AK^2.\)
Thành thử \(AL^2+BH^2+CK^2=\frac{\left(AL^2+BL^2\right)+\left(BH^2+CH^2\right)+\left(CK^2+AK^2\right)}{2}\ge\frac{AB^2+BC^2+CA^2}{2}.\)
Dấu bằng xảy ra khi \(AL=BL,BH=CH,CK=AK\Leftrightarrow I\) là giao điểm ba đường trung trực.
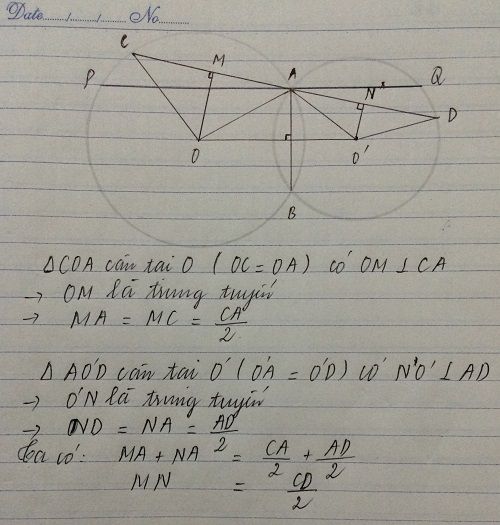
ấn đúng 0 ko là có cách