Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

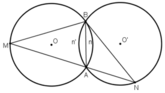
+ (O) và (O’) là hai đường tròn bằng nhau
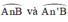 cùng được căng bởi dây AB
cùng được căng bởi dây AB
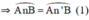
+ (O) có 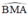 là góc nội tiếp chắn cung
là góc nội tiếp chắn cung 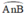
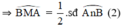
+ (O’) có 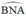 là góc nội tiếp chắn cung
là góc nội tiếp chắn cung 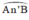
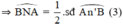
Từ (1); (2); và (3) suy ra 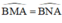
⇒ ΔBMN cân tại B.
Kiến thức áp dụng
+ Trong cùng một đường tròn hoặc hai đường tròn bằng nhau, hai dây bằng nhau căng hai cung bằng nhau.
+ Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.


Do hai đường tròn bằng nhau nên hai cung nhỏ AB bằng nhau. Vì cùng căng dây AB.
Suy ra  =
= 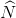 (cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B
(cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B

a: góc BMA=góc CNA=90 độ
=>MB//NC
=>IK//MB//NC
=>IK vuông góc MN
góc AIK+góc AHK=90+90=180 độ
=>AHIK nội tiếp
b: ΔHMN đồng dạng với ΔABC
=>góc MHN=góc BAC cố định
\(S_{HMN}=\dfrac{1}{2}\cdot HM\cdot HN\cdot sin\widehat{MHN}< =\dfrac{1}{2}\cdot AB\cdot AC\cdot sin\widehat{BAC}\)
Dấu = xảy ra khi MH là đừog kính của (O) và NH là đường kính của (O')

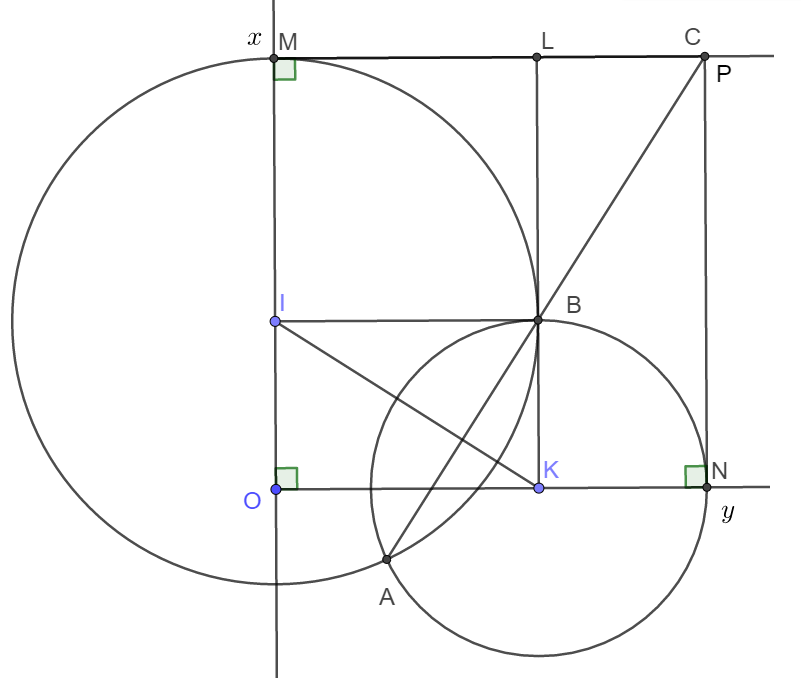
a) Trong tam giác OIK có:
|OK −− OI| < IK < |OK + OI| hay ∣R−r∣<IK<∣R+r∣∣R−r∣<IK<∣R+r∣.
Vậy hai đường tròn (I) và (K) luôn cắt nhau.
b) Dễ thấy tứ giác OMCN là hình chữ nhật (Tứ giác có 3 góc vuông).
Mà OM = OI + IM = OI + OK;
ON = OK + KN = OK + OI.
Vậy OM = ON hay hình chữ nhật OMCN là hình vuông.
c) Gọi giao điểm của BK và MC là L và giao điểm của AB với MC là P.
Tứ giác IBKO là hình chữ nhật. Suy ra IB = OK.
Tứ giác MLBI là hình vuông nên ML = BI, BL = OK.
Từ đó suy ra ΔBLP=ΔKOIΔBLP=ΔKOI. Vì vậy LP = OI.
Suy ra MP = ON = MC. Hay điểm C trùng với P.
Suy ra ba điểm A, B, C thẳng hàng.
d) Nếu OI + OK = a (không đổi) thì OM = MC = a không đổi. Suy ra điểm C cố định.
Vậy đường thẳng AB luôn đi qua điểm C cố định.

Xét tứ giác ACDB có A,C,D,B cùng nằm trên (O)
nên ACDB là tứ giác nội tiếp
=>\(\widehat{CAB}+\widehat{CDB}=180^0\)
mà \(\widehat{CAB}+\widehat{MAC}=180^0\)(hai góc kề bù)
nên \(\widehat{MAC}=\widehat{CDB}=\widehat{MDB}\)
Xét tứ giác AEFB có A,E,F,B cùng nằm trên (O')
nên AEFB là tứ giác nội tiếp
=>\(\widehat{BAE}+\widehat{BFE}=180^0\)
mà \(\widehat{BAE}+\widehat{MAE}=180^0\)(hai góc kề bù)
nên \(\widehat{MAE}=\widehat{MFB}\)
Xét ΔMCA và ΔMBD có
\(\widehat{MAC}=\widehat{MDB}\)
\(\widehat{M}\) chung
Do đó: ΔMCA đồng dạng với ΔMBD
=>\(\dfrac{MC}{MB}=\dfrac{MA}{MD}\)
=>\(MC\cdot MD=MA\cdot MB\)(1)
Xét ΔMAE và ΔMFB có
\(\widehat{MAE}=\widehat{MFB}\)
\(\widehat{M}\) chung
Do đó: ΔMAE đồng dạng với ΔMFB
=>\(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)
=>\(MA\cdot MB=MF\cdot ME\left(2\right)\)
Từ (1) và (2) suy ra \(MC\cdot MD=ME\cdot MF\)
=>\(\dfrac{MC}{MF}=\dfrac{ME}{MD}\)
Xét ΔMCE và ΔMFD có
\(\dfrac{MC}{MF}=\dfrac{ME}{MD}\)
\(\widehat{CME}\) chung
Do đó: ΔMCE đồng dạng với ΔMFD
=>\(\widehat{MCE}=\widehat{MFD}\)
mà \(\widehat{MCE}+\widehat{DCE}=180^0\)(hai góc kề bù)
nên \(\widehat{MFD}+\widehat{DCE}=180^0\)
=>CDFE là tứ giác nội tiếp

+ (O) và (O’) là hai đường tròn bằng nhau
+ (O) có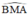 là góc nội tiếp chắn cung
là góc nội tiếp chắn cung 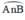
+ (O’) có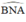 là góc nội tiếp chắn cung
là góc nội tiếp chắn cung 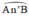
Từ (1); (2); và (3) suy ra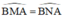
⇒ ΔBMN cân tại B.