Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x ' O y ' ^ = 30 ° , x ' O y ^ = 150 ° , x O y ' ^ = 150 ° .

Trên hai nửa mặt phẳng đối nhau bờ là đường thẳng yy' có:
hai tia Ox, Ox' và xOy +x'Oy=60*+60*=120*<180*
=>Tia Oy nằm giữa hai tia Ox và Ox'
mà xOy=x'Oy=60*
=>Tia Oy là tia phân giác của xOx'

a) Ta có:
O1^ + O2^ = 180o (kề bù)
=> O1^ = 180o - O2^ (1)
và O3^ + O2^ = 180o (kề bù)
=> O3^ = 180o - O2^ (2)
Từ (1) và (2) => O1^ = O3^ (hay xOy^ = x'Oy'^)
b)
Ta có:
O1^ + O2^ = 180o (kề bù)
=> O2^ = 180o - O1^ (3)
và O1^ + O4^ = 180o (kề bù)
=> O4^ = 180o - O1^ (4)
Từ (3) và (4) => O2^ = O4^ (hay yOx'^ = xOy'^)
a)Góc xOy và xOy' là 2 góc kề bù
=>xOy+xOy'=180o (1)
Góc xOy' và x'Oy' là 2 góc kề bù
=>xOy'+x'Oy'=180o (2)
So sánh (1) và (2) ta có:
xOy+xOy'=xOy'+x'Oy' (3)
Từ (3) => xOy=x'Oy'
b) Chứng minh tương tự phần a thôi :)
Góc xOy và yOx' là 2 góc kề bù
=>xOy+yOx'=1800 (1)
Góc xOy và xOy' là 2 góc kề bù
=>xOy+xOy'=180o (2)
So sánh (1) và (2) ta có:
xOy+yOx'=xOy+xOy' (3)
Từ (3) => yOx'=xOy'


a) Các cặp góc kề bù trong hình vẽ là :
\(xOa\) và \(aOy\) \(;aOy\) và \(yOb\); \(yOb\) và \(bOx\) ; \(bOx\) và \(xOa\)
b) +) Tính \(aOy\)
Vì 2 góc \(xOa;aOy\) kề bù
\(\Leftrightarrow xOa+aOy=180^0\)
Mà \(xOa=50^0\)
\(\Leftrightarrow50^0+aOy=180^0\)
\(\Leftrightarrow aOy=130^0\)
+) Tính \(yOb\)
Vì \(yOb;aOy\) là 2 góc kề bù
\(\Leftrightarrow yOb+aOy=180^0\)
Mà \(aOy=130^0\)
\(\Leftrightarrow yOb+130^0=180^0\)
\(\Leftrightarrow yOb=50^0\)
+) Tính \(xOb\)
Vì 2 góc \(yOb;xOb\) kề bù
\(\Leftrightarrow yOb+xOb=180^0\)
Mà \(yOb=50^0\)
\(\Leftrightarrow50^0+xOb=180^0\)
\(\Leftrightarrow xOb=130^0\)
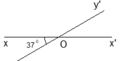
Ta có : xÔy + yÔx' = x'Ôx ( kề bù )
50o + yÔx' = 180o
yÔx' = 180o - 50o
yÔx' = 130o
Ta lại có : yÔx' + x'Ôy' = y'Ôy ( kề bù )
130o + x'Ôy' = 180o
x'Ôy' = 180o - 130o
x'Ôy' = 50o
Hoặc đơn giản là ta thấy yy' và xx' cắt nhau mà xÔy = 50o nên suy ra x'Ôy' = 50o
Ta có : xÔy + xÔy' = yÔy' ( kề bù )
50o + xÔy' = 180o
xÔy' = 180o - 50o
xÔy' = 130o