LY
và 
( m là tham số). Tìm 
để hai đường thẳng 
và 
song song nhau.
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2021
a.
Hai đường thẳng song song khi:
\(\dfrac{m+3}{2}=\dfrac{3}{2}\ne\dfrac{-2m+3}{2-3m}\)
\(\Leftrightarrow m=0\)
b.
Hai đường thẳng trùng nhau khi: \(\dfrac{m+3}{2}=\dfrac{3}{2}=\dfrac{-2m+3}{2-3m}\Rightarrow\) ko tồn tại m thỏa mãn
Vậy 2 đường thẳng cắt nhau khi \(m\ne0\)
CM
1 tháng 6 2018
Đáp án C
+Với m=1 ta có d: y=1 và d’: y=6
do đó hai đường thẳng này song song với nhau.
+ Với m =-1 ta có d: y= -2x-1 và d’: y= 6
suy ra hai đường thẳng này cắt nhau tại M(-7/2; 6)
+ Với m ≠ ± 1 khi đó hai đường thẳng trên là đồ thị của hàm số bậc nhất nên song song với nhau khi và chỉ khi:
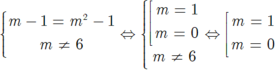
Đối chiếu với điều kiện m≠± 1 suy ra m= 0.
Vậy m= 0 và m= 1 là giá trị cần tìm.
Chọn C.
5 tháng 8 2021
a) Thay x=-1 và y=4 vào (d), ta được:
\(3m\cdot\left(-1\right)+m-2=4\)
\(\Leftrightarrow-2m=6\)
hay m=-3
b) Để (d)//(Δ) thì \(\left\{{}\begin{matrix}3m=6\\m-2\ne-1\end{matrix}\right.\Leftrightarrow m=2\)
CM
17 tháng 8 2019
Đáp án A
Do đường thẳng d song song với hai mặt phẳng (Oxy) và (Oxz).
Lại có: (Oxy) ∩ (Oxz) = Ox
Suy ra đường thẳng d song song với trục Ox.
Kết hợp với điểm O thuộc Ox, ta suy ra đường thẳng d không thể đi qua điểm O với mọi m. Vậy A là khẳng định sai.
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 4 2020
Để 2 đường thẳng trùng nhau \(\Rightarrow\left\{{}\begin{matrix}2k+6=-3\\2-m=m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=-\frac{9}{2}\\m=\frac{1}{2}\end{matrix}\right.\)
Để 2 đường thẳng song song \(\Rightarrow\left\{{}\begin{matrix}2k+6=-3\\2-m\ne m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=-\frac{9}{2}\\m\ne\frac{1}{2}\end{matrix}\right.\)
Để 2 đường thẳng cắt nhau \(\Rightarrow2k+6\ne-3\Rightarrow k\ne-\frac{9}{2}\)
Để 2 đường thẳng vuông góc \(\Rightarrow\left(2k+6\right).\left(-3\right)=1\Rightarrow k=-\frac{19}{6}\)
CM
28 tháng 6 2017
Chọn C.
d1 song song với d2 khi và chỉ khi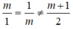 
khi đó ta có:
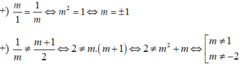
Vậy m = -1.
CM
10 tháng 1 2018
Hai đường thẳng song song khi m 3 = 2 − 4 ≠ − 3 2 n ê n m = − 3 2
Chọn đáp án C.