Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Số tam giác được tạo bởi 2 đỉnh trên d1 và 1 đỉnh trên d2 là: C 6 2 . C 4 1 = 60 . Số tam giác được tạo bởi 1 đỉnh trên d1 và 2 đỉnh trên d2 là: C 6 1 . C 4 2 = 36 . Do đó số tam giác được tạo thành là: 60 + 36 = 96. Xác suất cần tìm là: 60 96 = 5 8 .

Đáp án D
Lấy 2 đinh tô màu đỏ trong 6 điểm có C 6 2 cách
Lấy 1 đỉnh tô màu xanh trong 4 điểm có cách
Suy ra số tam giác tạo thành có 2 đỉnh tô màu đỏ là
C 6 2 . C 4 1 = 60
Vậy xác suất cần tính là
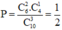

Chọn đáp án D
Lấy 2 đỉnh tô màu đỏ trong 6 điểm có C 6 2 cách.
Lấy 1 đỉnh tô màu xanh trong 4 điểm có cách.
Suy ra số tam giác tạo thành có 2 đỉnh tô màu đỏ là C 6 2 C 4 1 = 60
Vậy xác suất cần tính là
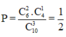

Chọn 3 điểm trong (n+10) điểm
chọn 3 điểm trong 10 điểm
chọn 3 điểm trong n điểm
=> số tam giác tạo thành là : \(C_{n+10}^3-C_{10}^3-C_{n}^3=2800\)
=> \(\frac{(n+8)(n+9)(n+10)}{3!}-120-\frac{(n-2)(n-1)n}{3!}=2800\)
=> n=20 => chọn B nha


Đáp án B
Phương pháp: Xác suất của biến cố A là n A n Ω trong đó nA là số khả năng mà biến cố A có thể xảy ra, n Ω là tất cả các khả năng có thể xảy ra.
Một tam giác được tạo thành khi nối ba điểm không thẳng hàng bất kì với nhau.
Cách giải
Số tam giác được tạo thành khi nối các điểm đó với nhau là:
Gọi biến cố A: “Tam giác có hai đỉnh màu đỏ”.
Khi đó n A = C 6 2 . C 4 1 = 60