Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hai đường thẳng lần lượt có vectơ chỉ phương là
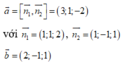
![]() nên d1 không vuông góc với d2
nên d1 không vuông góc với d2
![]()
Thay tọa độ x, y, z ở phương trình d2 vào phương trình của d1, ta được


Đường thẳng d qua M ( 2;-4;1 ) và có vectơ chỉ phương là u → 2 ; 3 ; 2
Đường thẳng d’ qua M' ( 0;1;-1 ) và có vectơ chỉ phương là u ' → = 4 ; 6 ; 4
Do u → và u ' → cùng phương đồng thời M ∉ d ' nên hai đường thẳng đó song song nhau.
Đáp án A

Chọn A
Ta có trung điểm của đoạn thẳng AB là điểm I(0;1;-1). Đường thẳng d có vecto chỉ phương là u=(1;-1;2). Vậy phưng trình đường thẳng đi qua trung điểm của đoạn thẳng
AB và song song với d là:
![]()

Ta có:
d 1 : x - 1 2 = y 1 = z + 2 - 2 có 1 véc tơ chỉ phương là: u 1 → 2 , 1 , - 2
d 2 : x + 2 - 2 = y - 1 - 1 = z 2 có 1 véc tơ chỉ phương là: u 2 → - 2 , - 1 , 2
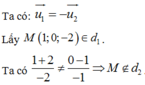
Vậy d 1 d 2 là hai đường thẳng song song
Chọn C




Đáp án A
Viết lại phương trình đường thẳng d 2 : x − 1 = y + 1 2 1 2 = z − 1 − 1 .
d 1 qua điểm A 2 ; 0 ; − 3 và có VTCP u 1 → = 2 ; − 1 ; 2 ;
d 2 qua điểm B 0 ; − 1 2 ; 1 và có VTCP u 2 → = − 1 ; 1 2 ; − 1 = − 1 2 2 ; − 1 ; 2 = − 1 2 u 1 → .
Mặt khác A 2 ; 0 ; − 3 ∉ d 2 .
Do đó d 1 / / d 2 .