Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
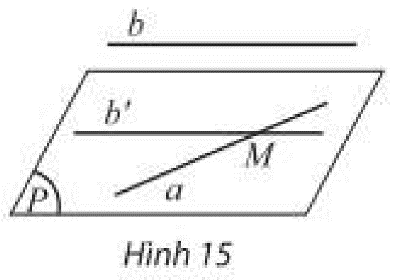
\(\left. \begin{array}{l}b\parallel b'\\b' \subset \left( P \right)\end{array} \right\} \Rightarrow b\parallel \left( P \right)\)
b) Theo hệ quả 1, ta có:
\(\left. \begin{array}{l}b\parallel \left( {P'} \right)\\M \in b'\\b\parallel b'\end{array} \right\} \Rightarrow b' \subset \left( {P'} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}a \subset \left( P \right)\\a \subset \left( {P'} \right)\end{array} \right\} \Rightarrow a = \left( P \right) \cap \left( {P'} \right)\\\left. \begin{array}{l}b' \subset \left( P \right)\\b' \subset \left( {P'} \right)\end{array} \right\} \Rightarrow b' = \left( P \right) \cap \left( {P'} \right)\end{array}\)
Do đó \(a\) và \(b'\) đều là các đường thẳng chung của hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\).
Vì \(a\) và \(b'\) phân biệt, mà hai mặt phẳng phân biệt chỉ có duy nhất một đường thẳng chung nên \(\left( P \right) \equiv \left( {P'} \right)\).

tham khảo:
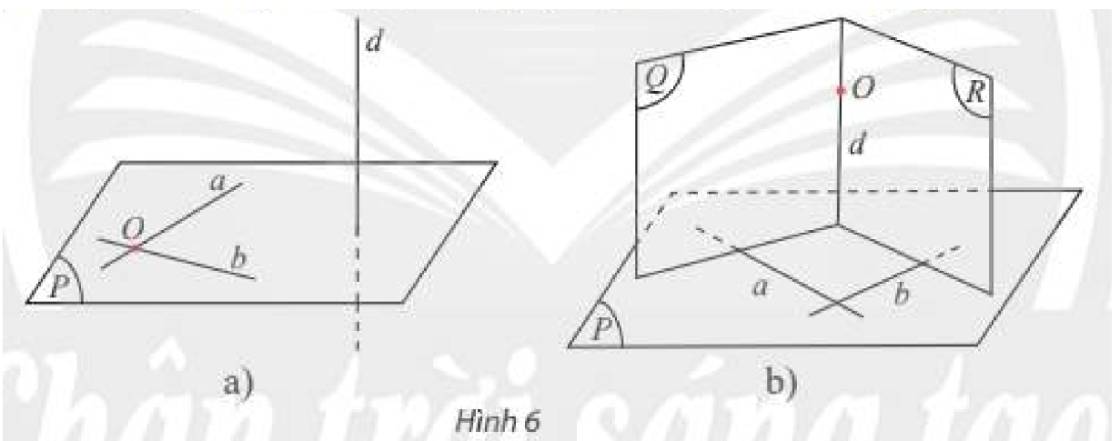
a) Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)
b) Vì a⊥(Q);d∈(Q) nên a⊥d
Vì b⊥(R),d∈(R) nên b⊥d
Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)

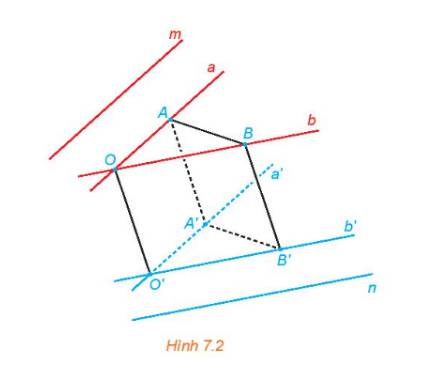
a) Mỗi cặp đường thẳng a, a' và b, b' cùng thuộc một mặt phẳng vì a // a', b // b'.
b) Ta có:
+) OA // O′A′; OO' // AA' nên OAA'O' là hình bình hành.
+) OB // O′B′; OO' // BB' nên OBB'O' là hình bình hành.
+) AB // A′B′ và OO' // AA'; OO' // BB' suy ra AA' // BB' nên ABB'A' là hình bình hành.
c) Áp dụng định lí côsin cho các tam giác OAB và O'A'B', ta có:
\(\cos \left( {a,b} \right) = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}};\cos \left( {a',b'} \right) = \frac{{O'{{A'}^2} + O'{{B'}^2} - A'{{B'}^2}}}{{2.O'A'.O'B'}}\)
Vì O'A' = OA và O'B' = OB; AB = A'B' nên cos(a,b) = cos(a′,b′).

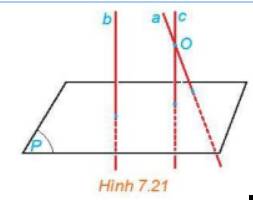
a) b // c; b ⊥ (P) ⇒ c ⊥ (P)
Mà a ⊥ (P)
a, c cùng đi qua điểm O
⇒ a trùng c.
b) Ta có b // c mà a trùng c nên a // b.

- Giả sử Δx là số gia của đối số tại xo = 1. Ta có:
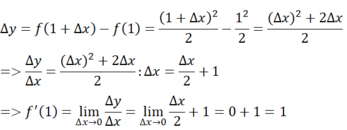
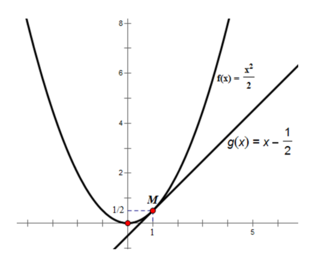
- Đường thẳng có hệ số góc bằng f'(1) = 1 có dạng:
y = 1.x + a hay y = x + a
Mà đường thẳng đó đi qua điểm M(1;1/2) nên có: 1/2 = 1 + a ⇒ a = 1/2 - 1 = -1/2
⇒ đường thẳng đi qua M và có hệ số góc bằng 1 là: y = x – 1/2
Ta có đồ thị như trên. Đường thẳng y = x – 1/2 tiếp xúc với đồ thị hàm số f(x) tại M

a) Qua điểm \(A\), ta vẽ được duy nhất một đường thẳng \(a\) song song với đường thẳng \(a'\).
Qua điểm \(A\), ta vẽ được duy nhất một đường thẳng \(b\) song song với đường thẳng \(b'\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}a\parallel a'\\a' \subset \left( Q \right)\end{array} \right\} \Rightarrow a\parallel \left( Q \right)\\\left. \begin{array}{l}b\parallel b'\\b' \subset \left( Q \right)\end{array} \right\} \Rightarrow b\parallel \left( Q \right)\end{array}\)
b) Ta có:
\(\left. \begin{array}{l}a\parallel \left( Q \right)\\b\parallel \left( Q \right)\\a,b \subset mp\left( {a,b} \right)\end{array} \right\} \Rightarrow mp\left( {a,b} \right)\parallel \left( Q \right)\)

tham khảo:
a) Vì M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) nên hình chiếu của a trên mặt phẳng (P) là a’ đường thẳng đi qua hai điểm M', N'.
b) b vuông góc với M'N' và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); M'N' cắt MM' tại M' do đó b vuông góc mặt phẳng tạo bởi M'N', MM' suy ra b có vuông góc với a.
c) b vuông góc với a và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); a cắt MM' tại M do đó b vuông góc mặt phẳng tạo bởi a, MM' suy ra b có vuông góc với M'N'.


Khi thay đổi vị trí của điểm $M$, góc giữa $a'$ và $b'$ sẽ không thay đổi. Điều này có nghĩa là cho dù ta di chuyển điểm $M$, hai đường thẳng $a'$ và $b'$ vẫn song song với nhau và góc giữa chúng không đổi.