Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giả sử a và b có vectơ chỉ phương là
. Lấy điểm A bất kì thuộc a và điểm B bất kì thuộc b. Với mỗi điểm M, gọi M' = (M) . Khi đó
=
. Suy ra
=
Ta có:
M ∈ a ⇔ cùng phương với
⇔
cùng phương với
⇔ M' ∈ b.
Từ đó suy ra phép tịnh tiến theo biến a thành b.
Vì A,B là các điểm bất kì (trên a và b tương ứng) nên có vô số phép tịnh tiến biến a thành b.
Giả sử a và b có vectơ chỉ phương là
. Lấy điểm A bất kì thuộc a và điểm B bất kì thuộc b. Với mỗi điểm M, gọi M' = (M) . Khi đó
=
. Suy ra
=
Ta có:
M ∈ a ⇔ cùng phương với
⇔
cùng phương với
⇔ M' ∈ b.
Từ đó suy ra phép tịnh tiến theo biến a thành b.
Vì A,B là các điểm bất kì (trên a và b tương ứng) nên có vô số phép tịnh tiến biến a thành b.
Đáp án A
Các phát biểuđúng: 2, 3,5,6
1. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó
4. Phép đối xứng tâm biến đường thẳng thành đường thằng song song hoặc trùng với nó
7. Phép biến hình F’ có được nhờ thực hiệnphép vị tựkhông phải là phép dời hình
Đáp án D
Phát biểuđúng: a , c, e, f, g, i, j, l
b. Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó có thể là phép tịnh tiến
d. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính
h. Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có AB = A’B’.
k. Nếu phép dời hình biến điểm A thành điểm B thì nó cũng biến điểm B thành A (phát biểu không đúng với phép tịnh tiến)
Đáp án C
Các phép biến hình luôn biến 1 đường thẳng thành 1 đường thẳng song song hoặc trùng với nó là: Tịnh tiến, đối xứng tâm, phép vị tự.
Đáp án D
Phép tịnh tiến theo các vectơ chỉ phương của d biến d thành d’
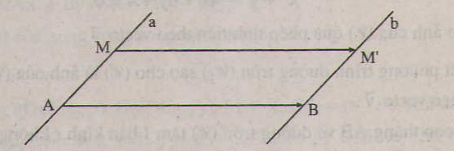
* Lấy A ∈ a và B ∈ b, lúc đó:
Phép tịnh tiến vectơ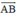
biến a thành b.
* Vì có vô số cách chọn A ∈ a và B ∈ b nên có vô số phép tịnh tiến biến a thành b.