Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

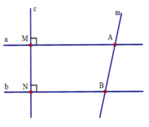
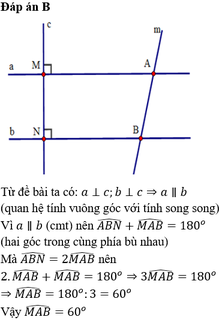
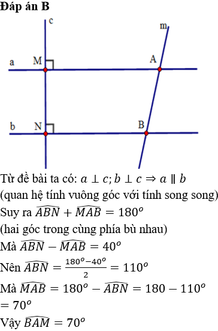
Từ đề bài ta có: a ⊥ c, b ⊥ c ⇒ a // b (quan hệ từ vuông góc đến song song)
⇒ ∠ABN + ∠MAB = 180° (hai góc trong cùng phía bù nhau)
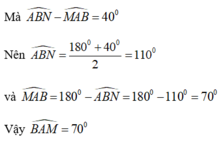
Chọn đáp án B.

(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
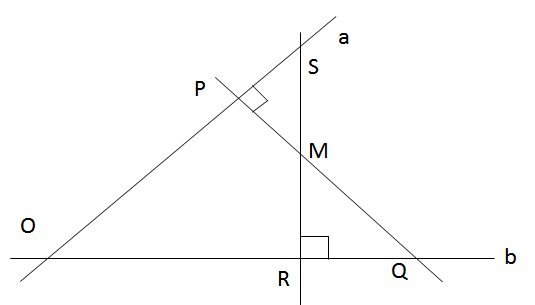
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b

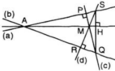
Gọi A là giao điểm của a và b.
Theo giả thiết c ⟘ a hay SR ⟘ AQ hay SR là đường cao của ΔASQ.
d ⟘ b hay PQ ⟘ AS hay QP là đường cao của ΔASQ.
SR cắt QP tại M ⇒ M là trực tâm của ΔASQ
⇒ AM ⟘ SQ
Vậy đường thẳng đi qua M và vuông góc với SQ cũng đi qua A (đpcm).
(BẠN TỰ VẼ HÌNH NHÉ)
Vì a vuông góc với c, b vuông góc với c=> a//b (tiên đề Ơ-clit)
Vì a//b (cmt) => Góc MAB + góc ABN = 180o (2 góc trong cùng phía).
Mà góc ABN = 2MAB (2 lần góc MAB)
=> ∠ MAB + 2MAB = 180o
3MAB = 180o=> MAB = 180o : 3 = 60o
Vậy ∠MAB = 60o