Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng tính chất 2, ta có \(\left( P \right)\) là mặt phẳng duy nhất đi qua ba điểm phân biệt \(A,B,C\) là mặt phẳng \(M,N,O\).
Áp dụng tính chất 3, ta có
– Đường thẳng \(a\) có hai điểm phân biệt \(M,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(a\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(a\) nằm trong mặt phẳng \(\left( P \right)\).
– Đường thẳng \(b\) có hai điểm phân biệt \(N,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(b\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(b\) nằm trong mặt phẳng \(\left( P \right)\).

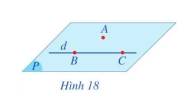
a) Mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d
b) Có một và chỉ một mặt phẳng đi qua điểm A và đường thẳng d

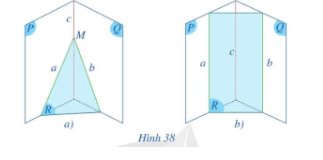
– Ta có: a ∩ b = {M}
Mà a ⊂ (P); b ⊂ (Q)
Nên M ∈ (P) và M ∈ (Q)
Do đó M là giao điểm của (P) và (Q).
Mà (P) ∩ (Q) = c, suy ra M ∈ c.
Vậy đường thằng c đi qua điểm M.
– Giả sử trong mặt phẳng (P) có a ∩ c = {N}.
Khi đó N ∈ a mà a ⊂ (R) nên N ∈ (R)
N ∈ c mà c ⊂ (Q) nên N ∈ (Q)
Do đó N là giao điểm của (R) và (Q).
Mà (Q) ∩ (R) = b

Đáp án A
Mặt phẳng ( α ) chứa điểm M và đường thẳng a
Mặt phẳng ( β ) chứa điểm M và đường thẳng b
Xét ( α ) và ( β ) có:
Điểm M là điểm chung
2 đường thẳng a và b chéo nhau
⇒ Tồn tại 1 giao tuyến duy nhất đi qua điểm M và cắt 2 đường thẳng a, b

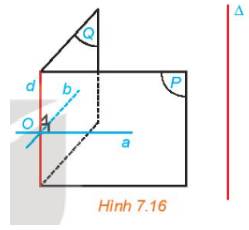
\(\left. \begin{array}{l}a \bot d\\d//\Delta \end{array} \right\} \Rightarrow \Delta \bot a\)
\(\left. \begin{array}{l}b \bot d\\d//\Delta \end{array} \right\} \Rightarrow \Delta \bot b\)
Mà \(a \cap b = \left\{ O \right\}\) \( \Rightarrow \) mp(a, b) đi qua O và vuông góc với \(\Delta \).

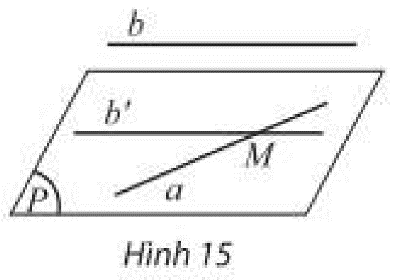
a) Ta có:
\(\left. \begin{array}{l}b\parallel b'\\b' \subset \left( P \right)\end{array} \right\} \Rightarrow b\parallel \left( P \right)\)
b) Theo hệ quả 1, ta có:
\(\left. \begin{array}{l}b\parallel \left( {P'} \right)\\M \in b'\\b\parallel b'\end{array} \right\} \Rightarrow b' \subset \left( {P'} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}a \subset \left( P \right)\\a \subset \left( {P'} \right)\end{array} \right\} \Rightarrow a = \left( P \right) \cap \left( {P'} \right)\\\left. \begin{array}{l}b' \subset \left( P \right)\\b' \subset \left( {P'} \right)\end{array} \right\} \Rightarrow b' = \left( P \right) \cap \left( {P'} \right)\end{array}\)
Do đó \(a\) và \(b'\) đều là các đường thẳng chung của hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\).
Vì \(a\) và \(b'\) phân biệt, mà hai mặt phẳng phân biệt chỉ có duy nhất một đường thẳng chung nên \(\left( P \right) \equiv \left( {P'} \right)\).

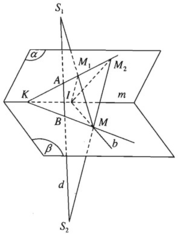
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.

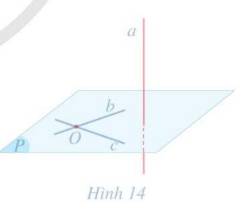
*Tìm giao tuyến của 2 mặt phẳng (M,a) và (M,b):
Có M là một điểm chung
Theo bài : a và b cắt nhau tại O
=> O thuộc a ⊂ (M,a) =>O thuộc (M,a)
và O thuộc b ⊂ (M,b) =>O thuộc (M,b)
=>O là điểm chung thứ hai
Vậy: (M,a) ∩ (M,b) = OM
Do đó giao tuyến OM lun thuộc mặt phẳng tạo bởi c và O ( mp (O,c)) là một mp cố định.
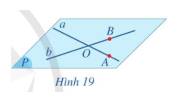

a) Mặt phẳng đi qua ba điểm A. B, O đi qua hai đường thẳng a và b
b) Có một và chỉ một mặt phẳng đi qua hai đường thẳng a và b