Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
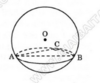
Gọi I là tâm mặt cầu đi qua hai điểm A, B cố định và phân biệt thì ta luôn có IA = IB. Do đó I thuộc mặt phẳng trung trực của đoạn AB.

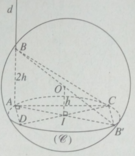
Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).

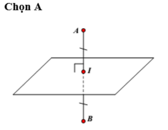
Gọi I là trung điểm của đoạn AB
⇒ I ( - 1 ; 1 ; - 1 )
Mặt phẳng trung trực của đoạn AB qua điểm I và nhận vecto A B → =(-4;-2;4) làm một vecto pháp tuyến. Phương trình mặt phẳng trung trực của AB là :
-4(x+1) - 2(y-1) + 4(z+1)=0
2x+y-2z-z=0

Đáp án là A
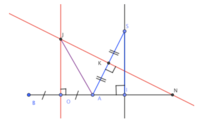
* Gọi J là tâm mặt cầu qua đường tròn tâm O và điểm S => J nằm trên đường trung trực của AB và SA
*Tam giác SIA vuông tại I.
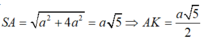
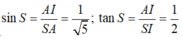
*Ta có: Góc N và S bằng nhau vì cùng phụ với góc S A N ^
* Tam giác AKN vuông tại K
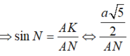
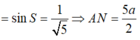
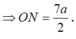
* Tam giác OJN vuông tại O
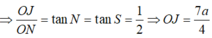
* Tam giác AOJ vuông tại O
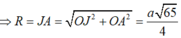
Cách 2
Gắn hệ trục toạ độ Oxy sao cho A, B, O thuộc tia Ox, S thuộc tia Oy và giả sử a = 1.
Khi đó A(1;0), B(3;0), S(0;2)
![]()
là đường tròn tâm J qua 3 điểm A, S, B
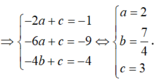
Suy ra:
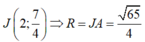
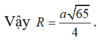

Đáp án A
Mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB.



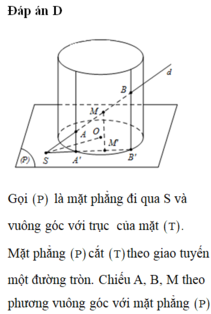

Ta có OA = OB nên tập hợp các tâm O của các mặt cầu đi qua hai điểm A, B là mặt phẳng trung trực của đoạn AB
Đáp án:B