Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha!!!
a.)Xét\(\Delta ABD\)và\(\Delta ABM\)có:
\(AD=BM\)
\(AB:\)Chung
\(\widehat{DAB}=\widehat{ABM}\left(slt\right)\)
\(\Rightarrow\Delta ABD=\Delta BAM\)
b.)Ta có:\(\Delta ABD=\Delta BAM\)(Theo a)
\(\Rightarrow\widehat{DBA}=\widehat{BAM}\)(mà 2 góc SLT)
\(\Rightarrow AM//BD\)
c.)Xét\(\Delta ADI\)và\(\Delta IMC\)có:
\(AD=CM\)
\(\widehat{DAI}=\widehat{IMC}\)
\(AI=IM\)
\(\Rightarrow\Delta AID=\Delta IMC\)
\(\Rightarrow IA=IC\)
\(\Rightarrow I\)là trung điểm của\(AC\)
\(\Rightarrow I,A,C\)thẳng hàng(đpcm)
P/s:#Study well#

a)Tam giác OAM và tam giác OBM có:
OA=OB(gt)
Góc MOA=góc MOB(Oz là tia pg của góc xOy)
OM là cạnh chung
Do đó tam giác OAM=tam giác OBM(c.g.c)
b)Ta có tam giác OAM=tam giác OBM(cmt)
=>Góc OAM=góc OBM và AM=BM
Tam giác AMC và tam giác BMD có:
AM=BM(gt)
góc CAM=góc DBM(cmt)
AC=DB(gt)
=>tam giác AMC=tam giác BMD(c.g.c)
=>góc AMC=góc BMD(2 góc tương ứng)
c)mik chưa nghĩ ra,xin lỗi nha![]()

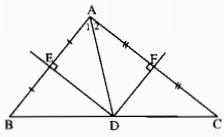
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b)
Ta có ∆DEB = ∆DEA(c.g.c) nên ˆB=ˆA1B^=A1^. Tương tự ˆC=ˆA2C^=A2^.
Suy ra ˆA=ˆA1+ˆA2=ˆB+ˆC

a) Vì d là đường trug trực của AB mà C,D thuộc d nên: AC=BC =>tam giác ACB cân tại C=> Góc CAB= góc CBA (1)
AD=BD=>tam giácABD cân tại D=> Góc DAB= góc DBA (2)
TỪ (1) và
Xét hai tam giác BAD và tam giác CAD, có:
BA=CA (do A thuộc đường trung trực của BC)
AD chung
BI=CI (do I thuộc đường trung trực BC)
Vậy tam giác BAD=tam giác CAD
Suy ra: góc BAD=góc CAD(hai góc tương ứng)
Vậy AD là tia phân giác của góc BAC (đpcm)