Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M. M chính là điểm cần tìm.
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA=MA’. Do đó : MA+MB=MA’+MB=A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A+M’B=M’A’+M’B lớn hơn hoặc bằng A'B. Dấu bằng chỉ xảy ra khi A’M’B thẳng hàng. Nghĩa là M trùng với M’

- Bước 1: Tìm điẻm A’ đối xứng với A qua đường thẳng d
- Bước 2: Nối A’B , đường thẳng này cắt d tại M . Là điểm cần tìm
- Bước 3: Chứng minh M là điểm duy nhất .
Study well

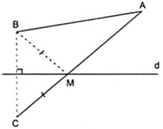
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d

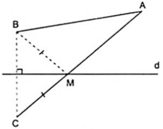
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d

Câu 2
Kẻ D doi xung voi A qua Ox
E doi xung voi A qua Oy
Goi B' la 1 diem bat ki tren Ox,C' la 1 diem bat ki tren Oy
Do Ox la duong trung truc cua AD
=> BA=BD,B'A=B'A
Tuong tu=> C'A=C'E,CA=CE
Ta co
PABC=AB+BC+AC
Ma AB=BD.AC=CE
=>PABC=BC+BD+CE=ED
lai co B'D+B'E\(\ge ED\)
B'C'\(\ge B'E\)
=> B'D+B'C'+C'E\(\ge ED\)
=>PAB'C'\(\ge P_{ABC}\)
Dau ''='' xay ra khi B'\(\equiv B,C'\equiv C\)
Gọi A' đối xứng A qua a
Nối A'B cắt a tại M thì \(AM+MB\) bé nhất
Giải thích:
Vì A' đx A qua a nên \(AM=A'M\)
Do đó \(AM+BM=A'M+BM\)
Để tổng trên nhỏ nhất thì 3 điểm A',M,B thẳng hàng hay A'B cắt a tại M